IJGIS：第二维度异常与空间预测
IJGIS 发布新空间预测方法：第二维度异常与空间预测。作者：任凯博士，宋泳泽副教授，于强研究员
澳大利亚科廷大学和西北农林科技大学联合培养博士任凯（现南京师范大学）、与导师科廷大学宋泳泽副教授、西北农林科技大学于强研究员，在国际一区期刊International Journal of Geographical Information Science (IJGIS) 发表论文 “Second-dimension outliers for spatial prediction”（用于空间预测的第二维度异常方法）。论文提出了 “第二维度异常（SDO）” 的全新概念与模型，通过提取未知位置（即未采样的待预测位置）的局部空间异常值和异常强度信息显著提高了空间预测的精度。
论文引用
Ren, K., Song, Y., Yu, Q., 2025. Second‑dimension outliers for spatial prediction. International Journal of Geographical Information Science, pp.1‑28.
访问论文：https://doi.org/10.1080/13658816.2025.2580414
X post：https://x.com/renkaigis/status/1993208196354445740
摘要
空间预测可利用空间依赖、空间格局、空间变异性及协变量，准确估计未采样位置的属性，从而揭示复杂空间系统的特征并支持多样化的应用。然而，现有的空间预测方法往往忽略了采样点之外的地理与环境特征，尤其是空间异常点（spatial outliers），这对预测精度具有显著影响。
本研究提出了“第二维度异常值（Second-Dimension Outliers, SDO）”的概念，并构建了可在预测过程中融合未采样位置局地异常信息的 SDO 模型，以提高空间预测精度。SDO 模型生成的 SDO 变量能够刻画样点外部的地理与环境特征，从而在空间预测中提供额外信息。本文进一步将 SDO 框架与机器学习模型结合，构建了 SDO 支持向量机（SDO-SVM）模型，对澳大利亚小麦产量进行了预测，并通过交叉验证评估模型精度。
结果表明，SDO-SVM模型在空间预测中显著优于非空间的SVM 模型，其决定系数 R2 由 0.555 提升至 0.671，尤其在极值预测方面表现出更高的准确性。此外，本研究提出的局地异常强度指数可量化 SDO 的强度，从而实现更平滑、更精确的空间预测。SDO 概念为空间预测提供了一种创新的空间视角与新的解释维度，可更深入地理解局地异常对空间分布的影响，具有较强的稳健性和广泛的应用潜力，可为空间统计推断与地理计算等领域提供有效工具。
第二维度异常 SDO 方法介绍
图 1. 第二维度异常（SDO）模型的示意图。
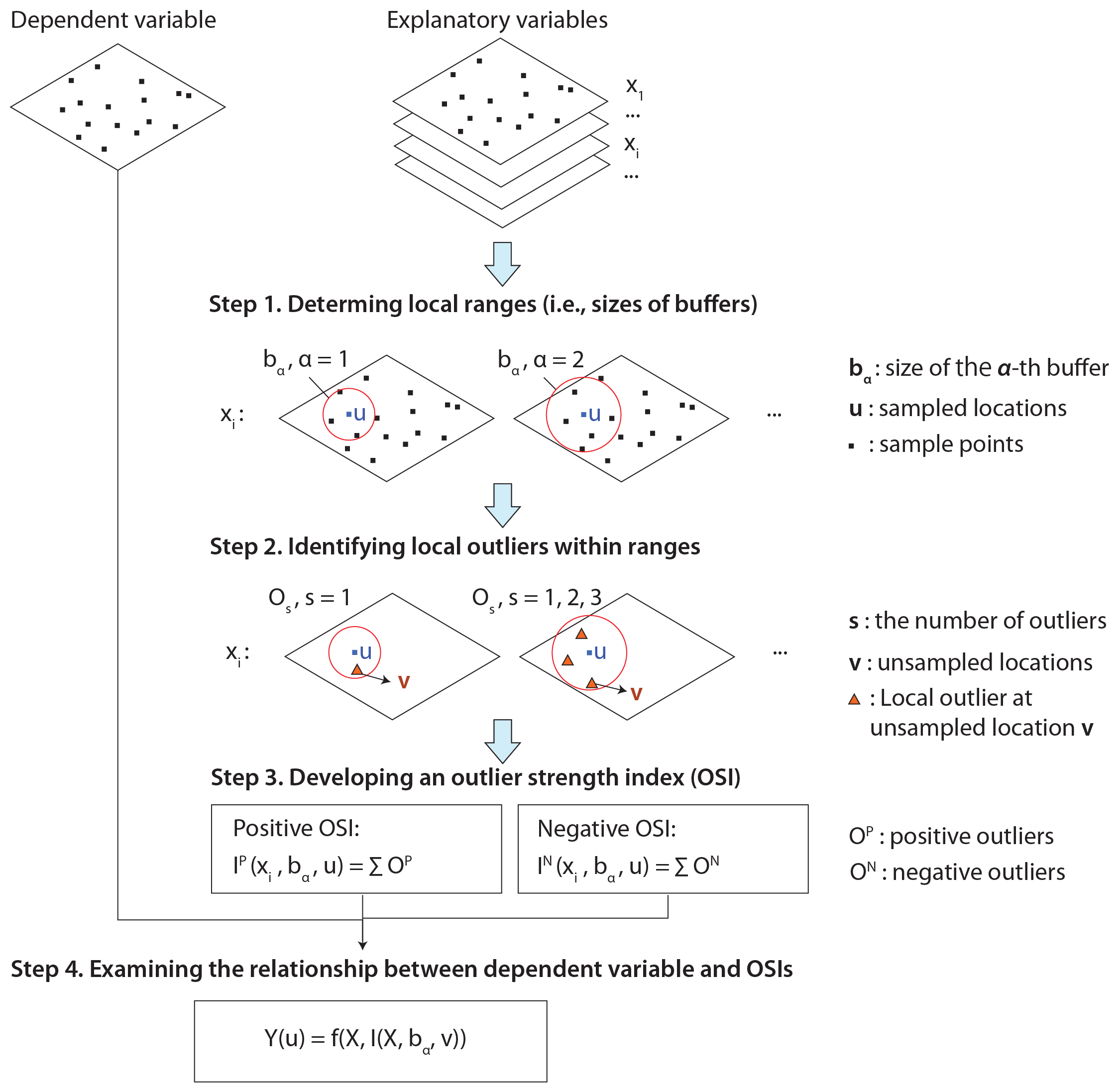
SDO 模型的构建主要包含四个步骤，如图1 ：
① 确定样本点局部邻域的缓冲区
根据研究区和样本点的空间特征和分布情况，确定一组局部缓冲区，包括缓冲区的大小、数量，以及缓冲区阈值，以更好地捕获更多的空间异常信息。同时也要避免样本量过小或者数据量过大，引入不必要的冗余信息。
② 识别不同缓冲区内的局部空间异常
在不同的缓冲区内，识别样本点周围未知位置处的局部异常点，这些异常点是基于其与预期值的偏差来定义的。正异常值为大于“平均值 + 2 倍标准差”，负异常值为小于“平均值 − 2 倍标准差”。识别异常值的标准差阈值可以根据数据的属性进行适当调整。
③ 构建异常强度指数 OSIs
在提取到未知位置处的异常信息后，通过累积不同缓冲区和空间尺度下的正负异常值，构建异常强度指数（Outlier strength index），即第二维度异常变量（SDO 变量）。
④ 建立因变量与 SDO 变量之间的关系
最后建立因变量与 SDO 变量之间的关系，将原有样本点的解释变量与 SDO 变量相结合，同时集成先进的机器学习回归算法，构建全新的空间预测模型。
模拟实验
研究以随机生成的 20*20 的格网区域内的数据点进行初步模型验证。采用 5 折交叉验证，使用 80% 的训练集，20% 的测试集来评估模型。
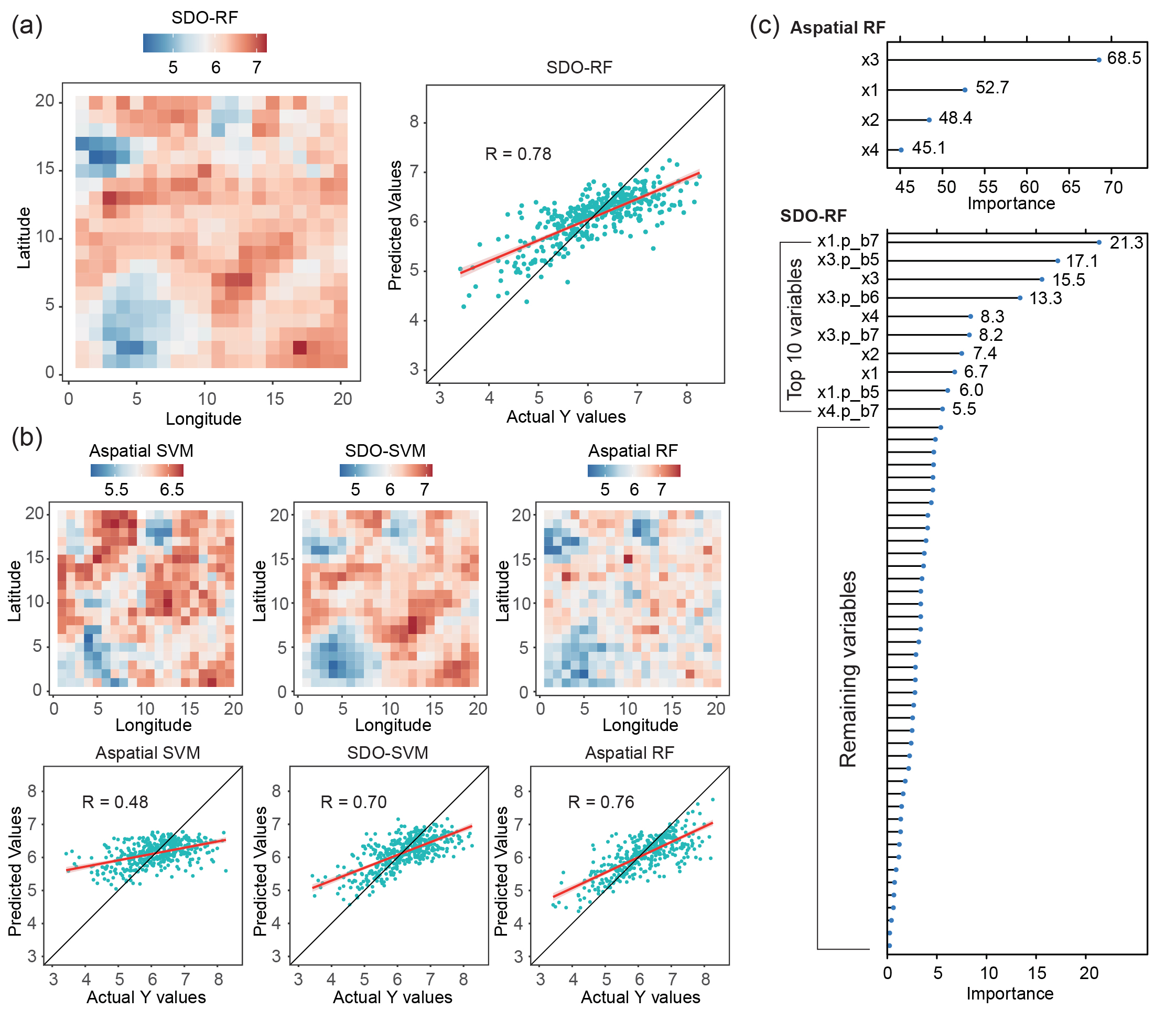图 2.使用随机森林（RF）和支持向量机模型（SVM）对模拟数据进行 SDO 建模的结果。（a）使用 RF 的 SDO 预测结果，（b）基于非空间的 RF、SVM 和 SDO-SVM 的预测结果，（c）非空间 RF 和 SDO-RF 模型单个变量的重要性。
模拟案例中使用的机器学习算法包括随机森林和支持向量回归算法，图2 展示了模拟数据的空间预测结果，可以看出引入 SDO 变量的机器学习方法的 Pearson 相关系数 R 都显著高于非空间机器学习方法，其中 SDO-RF 的空间预测效果最好，SDO-SVM 的 R 值从非空间 SVM 的 0.48 提高到 0.7，提升了 45.8%。同时根据 SDO-RF 和非空间 RF 的变量的重要性对比，x3 无论在哪种模型中，对因变量 y 的影响都是显著的。在 SDO 变量中，前十的贡献变量中有四个是 x3 及其 SDO 衍生变量，进一步验证了空间异常在提高预测准确性的优势。
澳大利亚小麦产量空间预测应用
研究使用 2021 年澳大利亚的小麦产量数据开展进一步的模型验证，样本点数据来自澳大利亚统计局，包含 179 个 LGA 区域（Local government area），研究尺度涵盖整个澳大利亚区域内的小麦带。解释变量包括影响小麦产量的一系列因子，包括气温，降水，蒸散发，NDVI，EVI，总磷，总氮，沙土含量，泥沙含量等。待预测格网则采用了 10km*10km 的空间分辨率。
为保证空间尺度和坐标系的一致性，所有数据的投影坐标系选择基于GDA1994基准的澳大利亚阿尔伯斯等积圆锥投影坐标系（GDA_1994_Australia_Albers (EPSG:3577)）。
案例实验的步骤如图3所示：
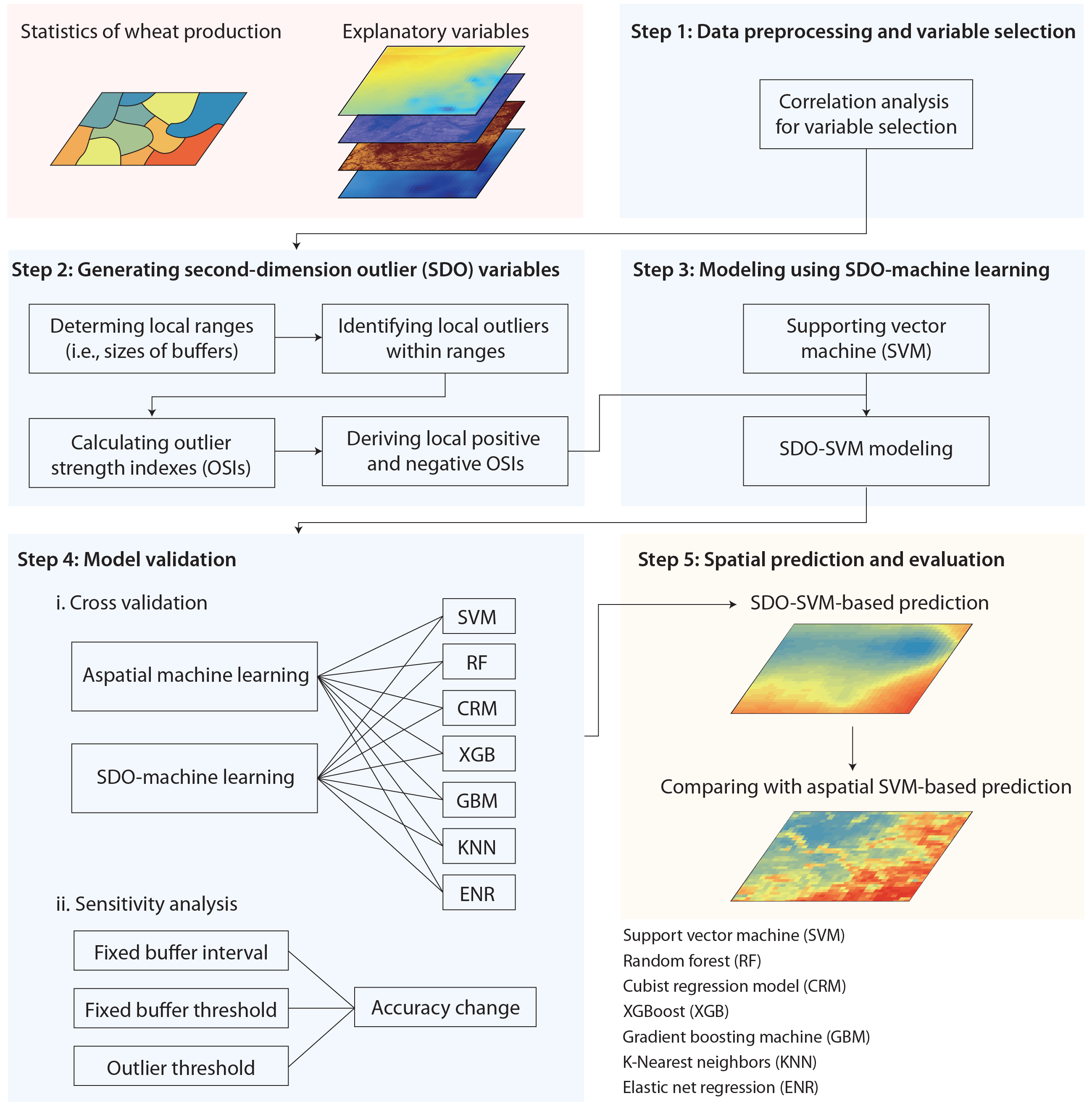图 3. 用于澳大利亚小麦产量预测的第二维度异常（SDO）模型的主要步骤。
首先进行数据预处理和变量选择，最终保留了9个解释变量。接着根据局部缓冲区的大小和数量，生成样本点局部邻域内的SDO变量。然后，将这些变量与原始变量结合，集成机器学习算法，构建SDO空间预测模型。在模型验证部分，我们采用了7种机器学习算法来共同评估SDO模型，其次还对SDO模型开展了敏感性分析。最后，通过对比SDO-SVM与非空间SVM模型的空间预测结果，进一步验证了本研究提出的SDO方法对于空间预测精度提升的重要作用。
如图4所示，我们生成了小麦带内气温的正/负SDO 变量，缓冲区设置为 100km 到 700km，间隔 100km，既保证了识别到足够多的异常信息，也避免了引入冗余数据。其他 8 个变量的 SDO 变量分布与气温类似。
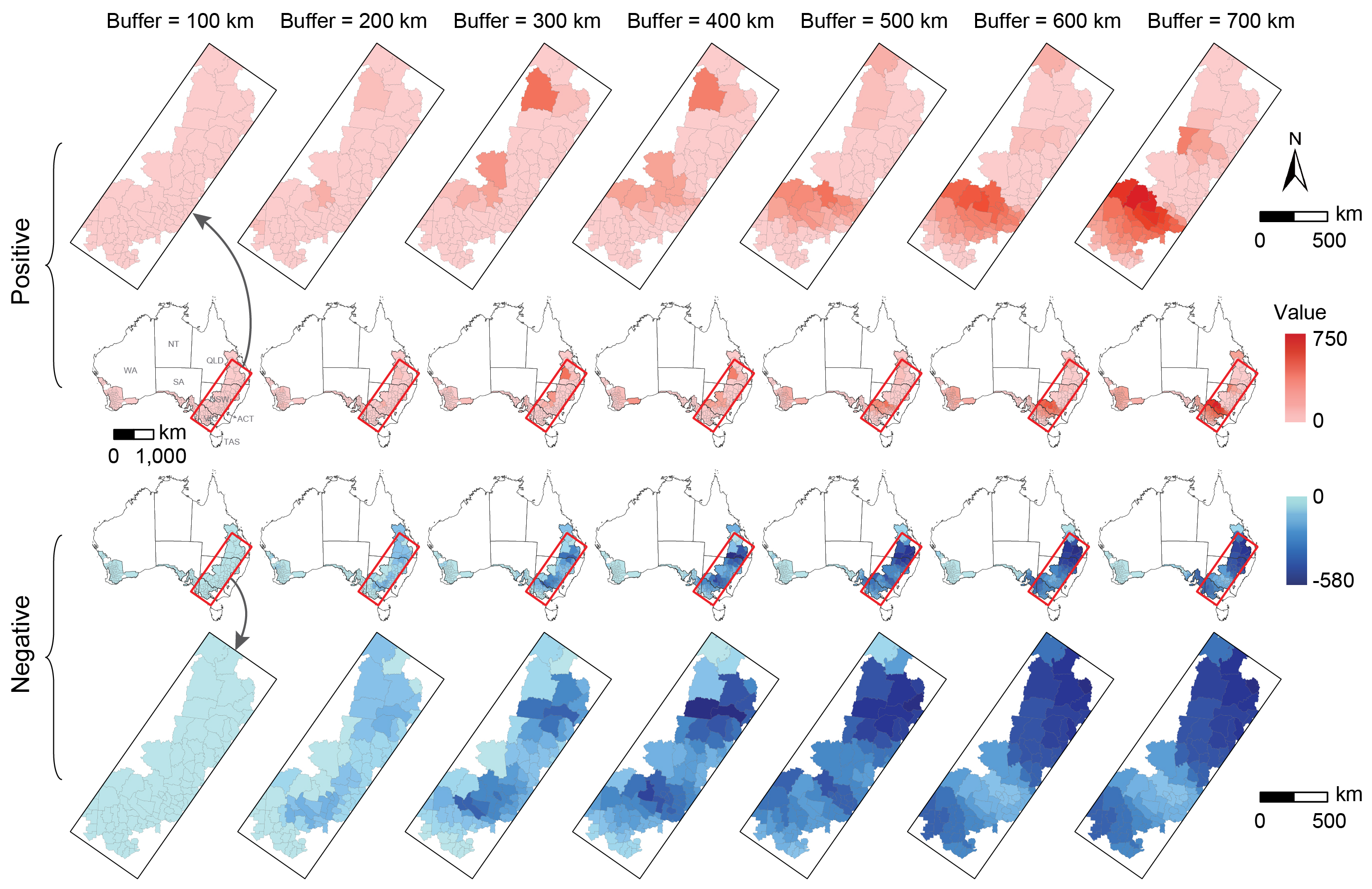图 4. SDO 模型在不同缓冲区下生成的第二维度温度变量的分布，包括正异常值（红色）和负异常值（蓝色）。
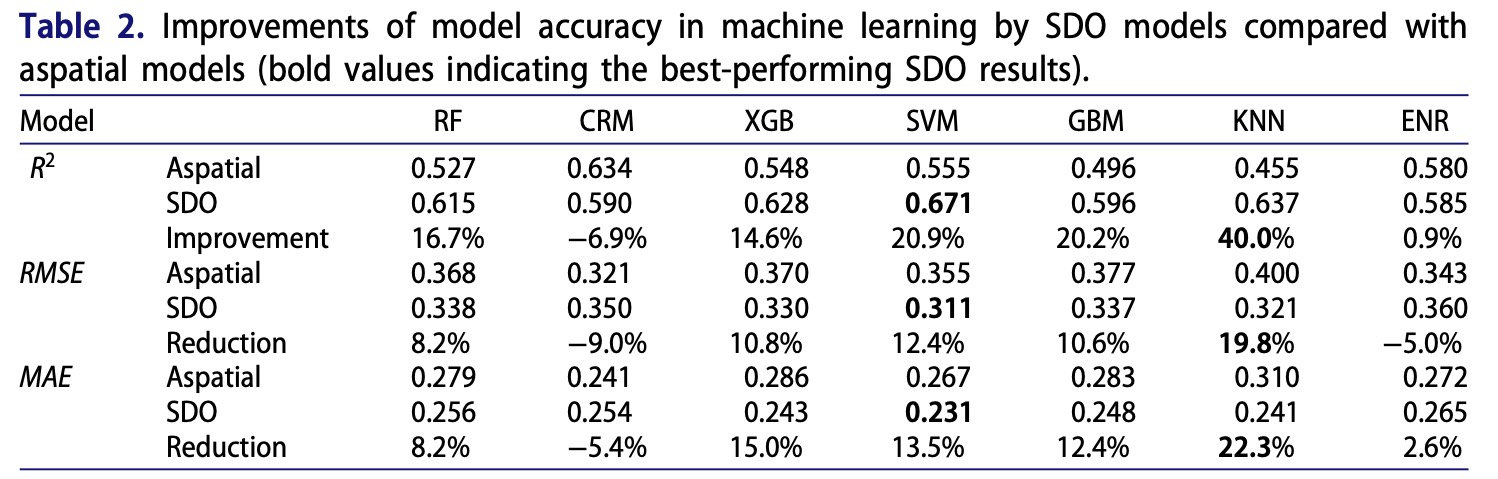
下表统计了 SDO 模型与 7 种机器学习算法相结合之后，预测精度的提升和误差降低的情况。引入第二维度异常的模型在不同程度上提升了精度和降低了误差，其中SVM 方法表现尤为突出，R2 从 0.555 到 0.671 提升了 20.9%，RMSE 和 MAE 也分别降低了 12.4% 和 13.5%。
图5 进行了 SDO 模型的敏感性分析，分别从缓冲区阈值，缓冲区间隔，和识别异常值的标准差阈值三个方面进行，不同参数下模型的 CV-RMSE 的变化均在 +/-5% 内，表明本研究的 SDO 模型对参数不敏感，具有一定的鲁棒性和泛化能力。
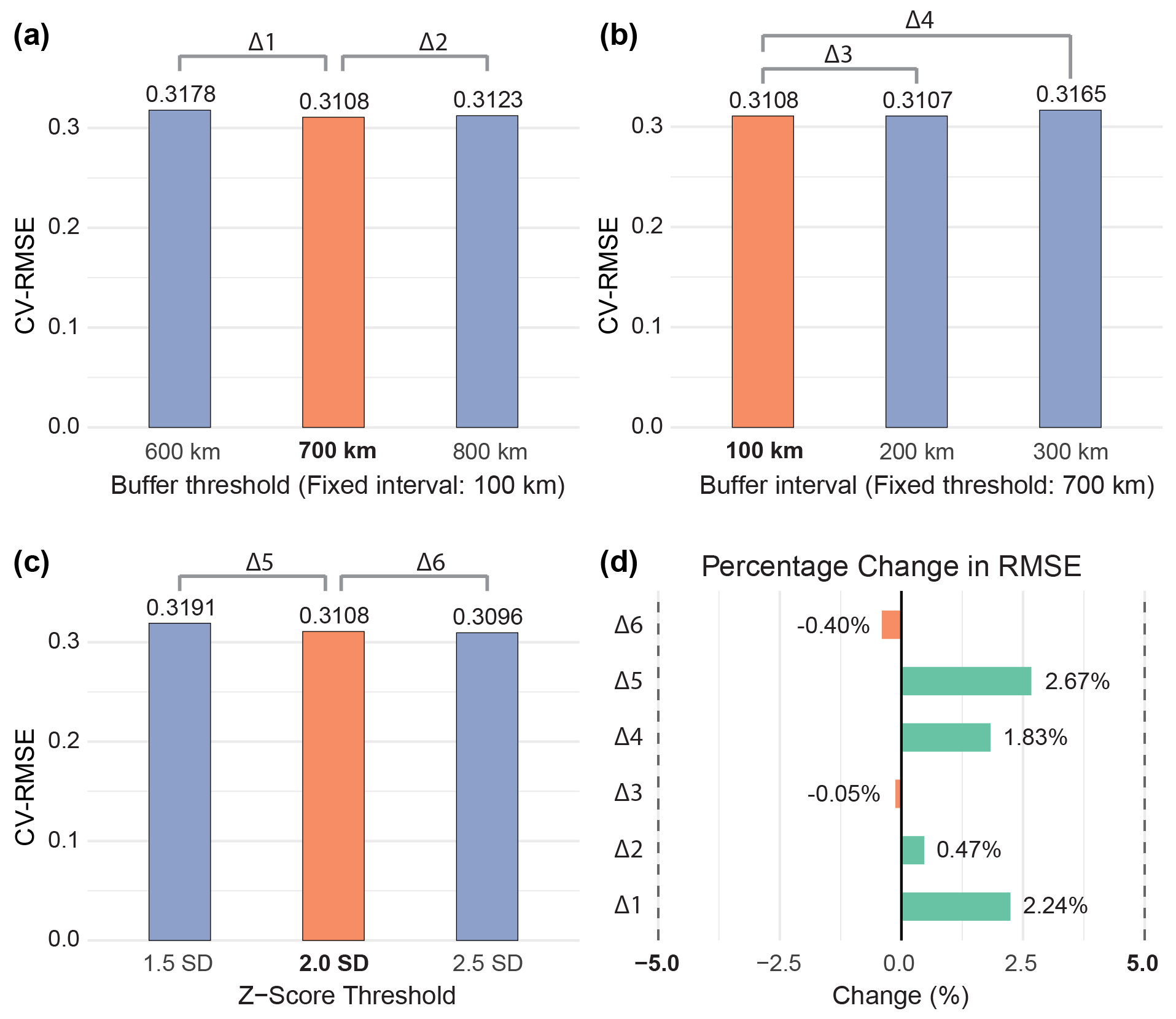图 5. SDO 模型的敏感性分析：缓冲阈值、缓冲间隔和离群值（标准差）阈值设置对模型准确度的影响（交叉验证均方根误差，CV-RMSE）。
图6 展示了澳大利亚小麦产量的空间预测结果，SDO-SVM 表现出更平滑和更连续的空间分布模式，同时也保留了局部变异性，其对于最大值和最小值的预测更为准确。图7 通过对新南威尔士州内小麦带横截面的预测结果对比，两种模型都有相同的空间趋势，但SDO-SVM 显示出更平滑的过渡和对最大值和最小值的敏锐预测。图8 进一步说明了这一点，SDO模型引入的空间异常信息增强了机器学习模型解释小麦产量精细尺度下的空间异质性的能力，尤其是对最大值和最小值这些易忽略的信息的捕捉。
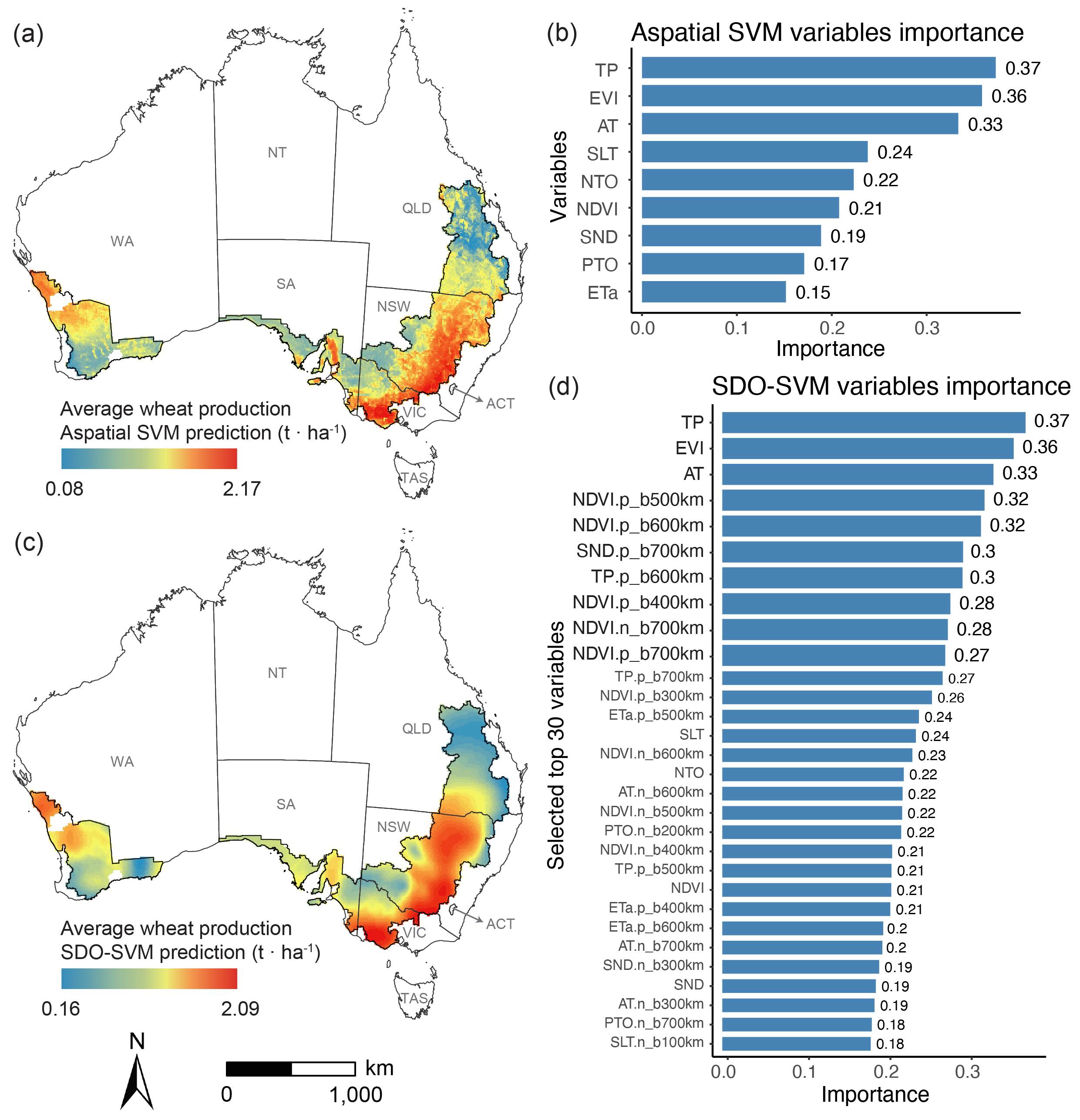图 6. 基于非空间模型（a）和 SDO 机器学习模型（c）的澳大利亚小麦产量预测结果，以及前 30 个 SDO 变量（d）和非空间变量（b）在机器学习模型中的重要性。
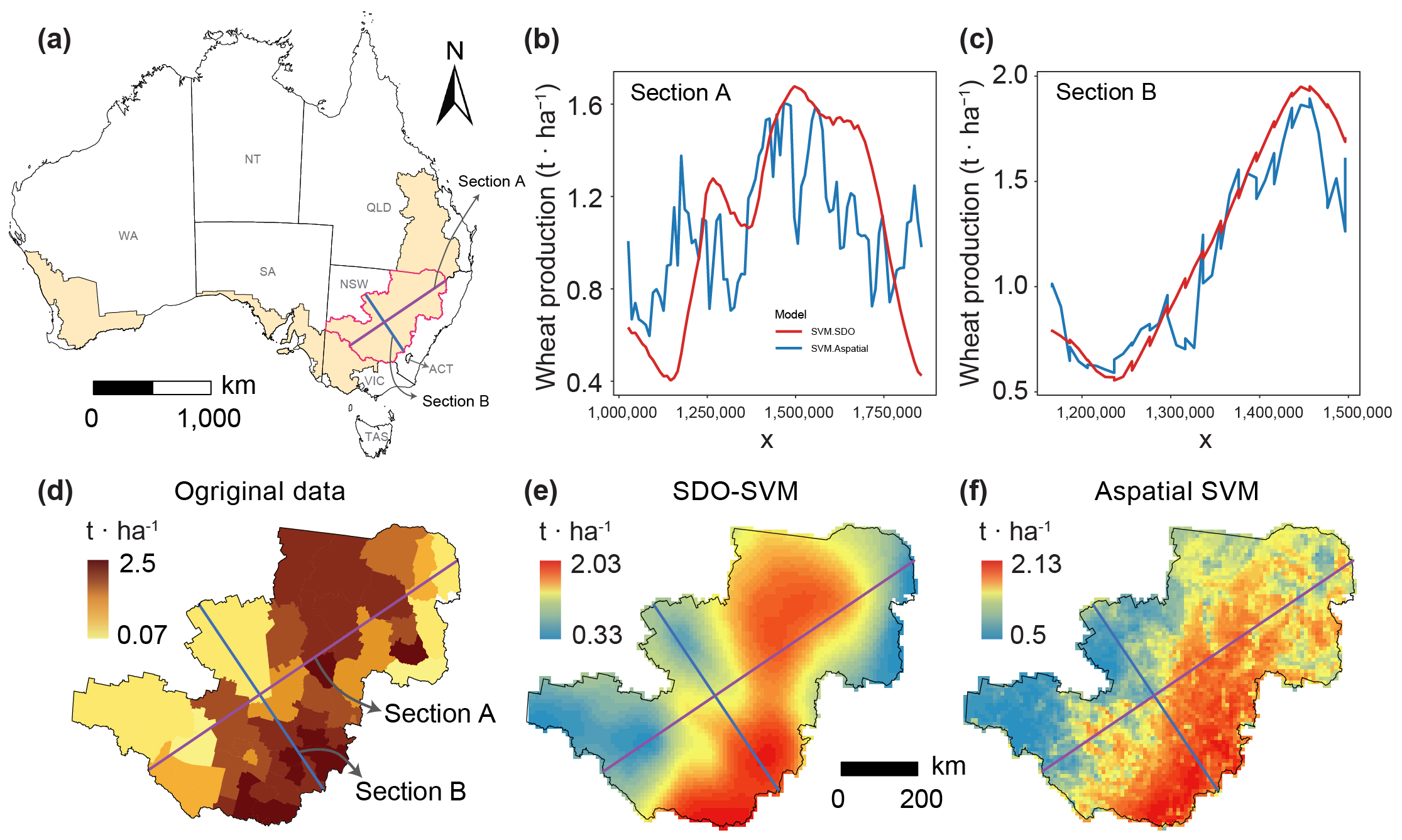图 7. 新南威尔士州小麦带内 SDO 模型和非空间模型沿着横截面预测结果的比较。（a）截面 A（西南至东北）和截面 B（西北至东南）在新南威尔士州的位置。（b，c）沿着 A 和 B 截面的 SDO-SVM 和非空间 SVM 小麦产量预测的折线图。（d）原始小麦产量数据。（e，f）SDO-SVM（e） 和非空间 SVM（f）的预测结果。
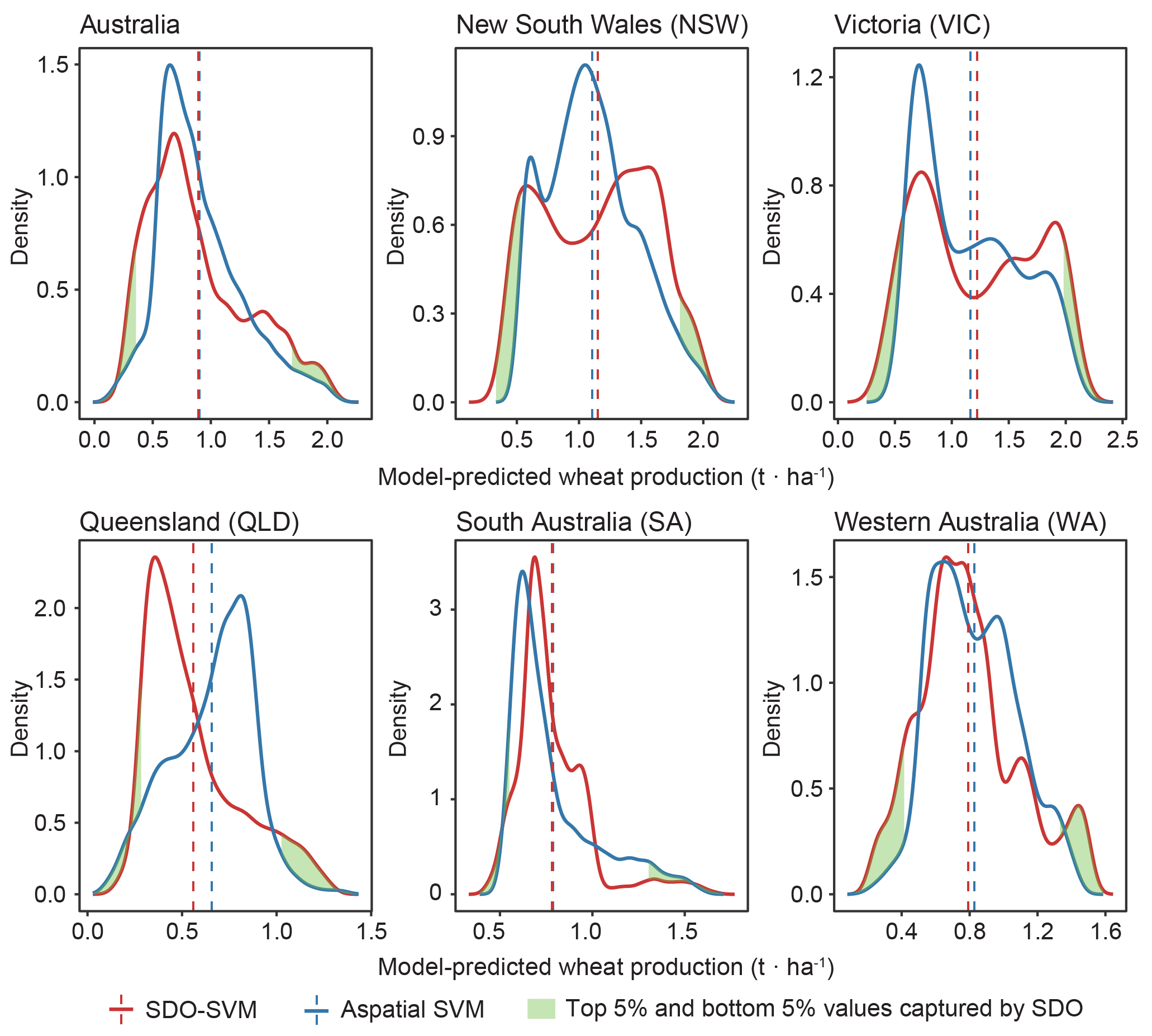图 8. 澳大利亚及各州的 SDO 和非空间模型的小麦产量预测结果的密度图。
综上，本研究提出的第二维度异常概念，在捕捉多尺度空间异常值方面具有较好的性能，通过提取样本点以外区域异常的地理和环境特征，显著提高了预测精度，避免了异常值信息的模糊，减少了预测误差，从而为空间统计推断与地理计算提供更具解释力和更高可靠性的创新方法。
本研究一作任凯的个人公众号：
