空间插值的确定性方法【R】
作为风险评估的一个组成部分,用于预测未采样位置的值的空间插值技术已被广泛用于绘制环境变量,以识别针对管理干预措施的地理区域。空间插值方法可以分为两大类:
经典的空间自相关统计包括:
- 确定性或非地统计学方法
- 随机或地统计学方法
全部机翻,如有错误,以你的感觉为准。
空间插值的确定性方法
确定性插值技术 (也称为精确插值器) 基于相似程度 (反距离加权) 或平滑程度 (径向基函数) 来预测测点的值。这种插值技术通常在不记录潜在误差的情况下预测与采样位置处的测量值相同的值,或者假定误差可以忽略不计。
全局技术使用整个数据集 (多项式趋势面) 计算预测。局部技术从邻域内的测量点计算预测,邻域是较大研究区域内较小的空间区域。
在本练习中,我们将探索以下确定性方法来预测土壤有机碳:
- 多项式趋势面
- 邻近度分析-泰森多边形
- 最近邻插值
- 反距离加权
- 薄板样条插值
R 包
1
2
3
4
5
6
7
8
9
10
11
library(plyr)
library(dplyr)
library(gstat)
library(raster)
library(ggplot2)
library(car)
library(classInt)
library(RStoolbox)
library(spatstat)
library(dismo)
library(fields)
加载数据
1
2
3
4
5
6
7
# Define data folder
dataFolder<-"D:\\Env\\DATA_08\\"
train<-read.csv(paste0(dataFolder,"train_data.csv"), header= TRUE)
state<-shapefile(paste0(dataFolder,"GP_STATE.shp"))
grid<-read.csv(paste0(dataFolder, "GP_prediction_grid_data.csv"), header= TRUE)
p.grid<-grid[,2:3]
定义坐标
1
2
3
coordinates(train) = ~x+y
coordinates(grid) = ~x+y
gridded(grid) <- TRUE
多项式趋势面
多项式趋势曲面分析是最广泛使用的全局插值技术,其中使用最小二乘方程 (线性或二次方程) 拟合数据,然后基于该方程创建插值曲面。所得曲面的性质由多项式的阶数控制。
线性拟合
拟合一阶多项式模型:
SOC =intercept + aX+ bY (X = x coordinates, Y= y coordinates)
我们将在没有指定地理坐标的情况下使用 gstat 包的 krige() 函数。它将执行普通或加权最小二乘预测
1
2
model.lm<-krige(SOC ~ x + y, train, grid)
# [ordinary or weighted least squares prediction]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
summary(model.lm)
# Object of class SpatialPixelsDataFrame
# Coordinates:
# min max
# x -1250285 119715
# y 998795 2538795
# Is projected: NA
# proj4string : [NA]
# Number of points: 10674
# Grid attributes:
# cellcentre.offset cellsize cells.dim
# x -1245285 10000 137
# y 1003795 10000 154
# Data attributes:
# var1.pred var1.var
# Min. :2.726 Min. :23.89
# 1st Qu.:5.046 1st Qu.:23.94
# Median :6.480 Median :24.00
# Mean :6.190 Mean :24.03
# 3rd Qu.:7.254 3rd Qu.:24.10
# Max. :9.006 Max. :24.39
绘图
1
2
spplot(model.lm ,"var1.pred",
main= "1st Order Trend Surface")
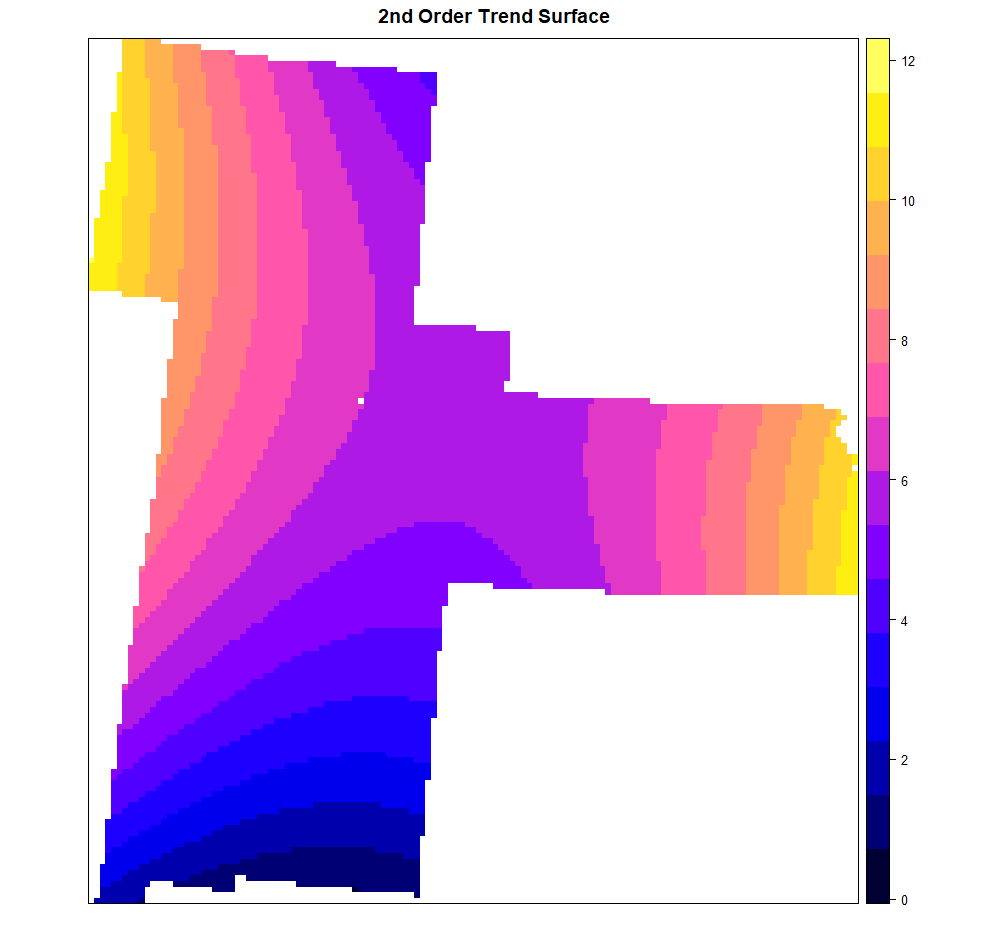
二次拟合
拟合二阶多项式模型:
SOC = x + y + I(x*y) + I(x^2) + I(y^2)
1
2
model.quad<-krige(SOC ~ x + y + I(x*y) + I(x^2) + I(y^2), train, grid)
# [ordinary or weighted least squares prediction]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
summary(model.quad)
# Object of class SpatialPixelsDataFrame
# Coordinates:
# min max
# x -1250285 119715
# y 998795 2538795
# Is projected: NA
# proj4string : [NA]
# Number of points: 10674
# Grid attributes:
# cellcentre.offset cellsize cells.dim
# x -1245285 10000 137
# y 1003795 10000 154
# Data attributes:
# var1.pred var1.var
# Min. : 0.6923 Min. :21.84
# 1st Qu.: 5.0919 1st Qu.:21.88
# Median : 6.0541 Median :21.96
# Mean : 6.1666 Mean :22.06
# 3rd Qu.: 7.5374 3rd Qu.:22.17
# Max. :11.5427 Max. :23.52
绘图
1
2
spplot(model.quad ,"var1.pred",
main= "2nd Order Trend Surface")
邻近度分析-泰森多边形
泰森多边形是最简单的插值方法,通过它我们可以在所有未采样的位置赋值,考虑到最近的采样位置的值。通过这种方式,我们可以定义相对于所有其他点最接近每个点的区域边界。它们在数学上由所有点之间的直线的垂线平分线来定义。
可以使用 R 中的 spatstat 的 dirichlet() 函数或 dismo 包的 voronoi() 函数创建泰森多边形。
在这里,我们将应用 dismo 包的 voronoi() 函数。
在创建泰森多边形之前,我们必须创建一个 SpatialPointsDataFrame。
1
2
3
4
5
6
7
8
9
10
df<-as.data.frame(train)
## define coordinates
xy <- df[,8:9]
SOC<-as.data.frame(df[,10])
names(SOC)[1]<-"SOC"
# Convert to spatial point
SPDF <- SpatialPointsDataFrame(coords = xy, data=SOC)
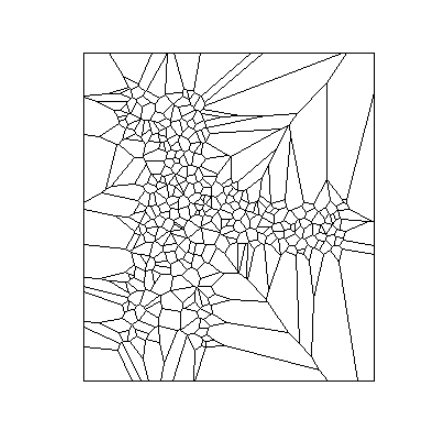
v <- voronoi(SPDF)
plot(v)
绘图看起来不太好,让我们限制在GP州的边界内。
1
2
3
4
# disslove inter-state boundary
bd <- aggregate(state)
# apply intersect fuction to clip
v.gp <- raster::intersect(v, bd)
现在我们绘制地图
1
2
3
spplot(v.gp, 'SOC',
main= "Thiessen polygons (Voronoi)",
col.regions=rev(get_col_regions()))
现在将这个 Voronoi 多边形转换为栅格(10 km x 10 km)
1
2
r <- raster(bd, res=10000)
vr <- rasterize(v.gp, r, 'SOC')
绘图
1
2
3
4
5
6
7
8
9
10
11
ggR(vr, geom_raster = TRUE) +
scale_fill_gradientn("SOC", colours = c("orange", "yellow", "green", "blue","sky blue"))+
theme_bw()+
theme(axis.title.x=element_blank(),
axis.text.x=element_blank(),
axis.ticks.x=element_blank(),
axis.title.y=element_blank(),
axis.text.y=element_blank(),
axis.ticks.y=element_blank())+
ggtitle("Thiessen polygons (Voronoi) of SOC")+
theme(plot.title = element_text(hjust = 0.5))
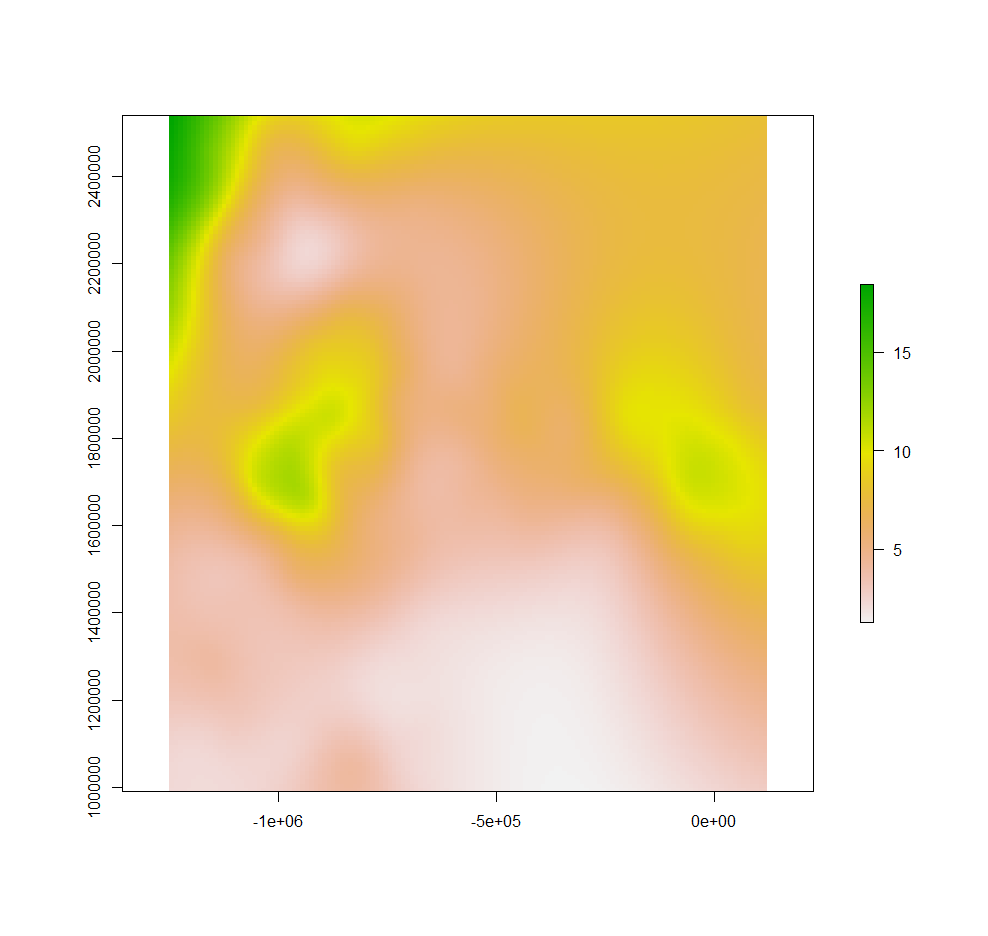
最近邻插值
在这里,我们考虑多个(5)临近值进行最近邻插值。
我们将使用 gstat 包使用最近邻插值对 SOC 进行插值。首先,我们使用 krige() 函数拟合一个模型 (~ 1表示) “仅截取”。在空间数据的情况下,将仅使用 “x” 和 “y” 坐标。我们将最大点数设置为 5,将 “反距离幂” idp 设置为零,这样所有五个邻居的权重都相等。
1
2
nn <- krige(SOC ~ 1, train, grid, nmax=5, set=list(idp = 0))
# [inverse distance weighted interpolation]
转换为栅格
1
2
3
# na.omit(<向量a>): 返回删除NA后的向量a
nn.na<-na.omit(nn)
nn.pred<-rasterFromXYZ(as.data.frame(nn)[, c("x", "y", "var1.pred")])
绘制最近邻预测 SOC
1
2
3
4
5
6
7
8
9
10
11
ggR(nn.pred, geom_raster = TRUE) +
scale_fill_gradientn("SOC", colours = c("orange", "yellow", "green", "sky blue","blue"))+
theme_bw()+
theme(axis.title.x=element_blank(),
axis.text.x=element_blank(),
axis.ticks.x=element_blank(),
axis.title.y=element_blank(),
axis.text.y=element_blank(),
axis.ticks.y=element_blank())+
ggtitle("Nearest Neighbour\n Predicted SOC")+
theme(plot.title = element_text(hjust = 0.5))
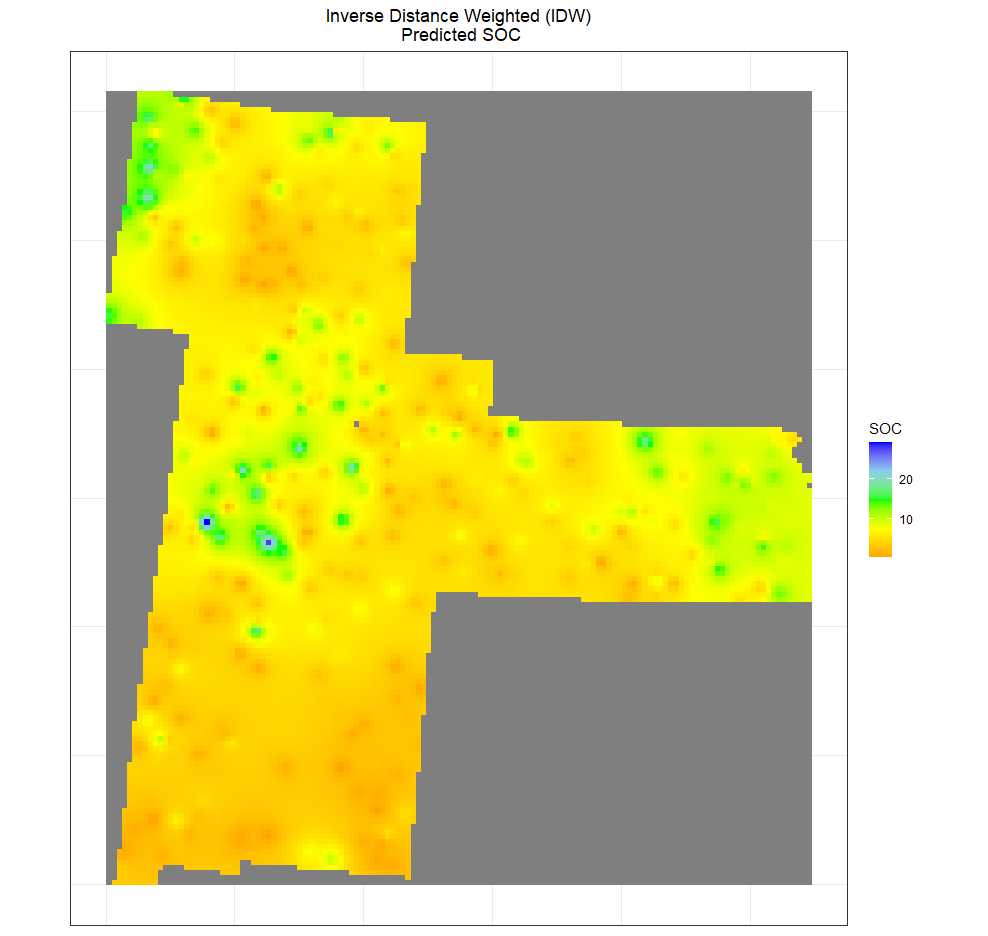
反距离加权插值
反距离加权 (IDW) 是一种最常用的非统计空间插值方法,该方法基于以下假设: 彼此接近的事物比相距更远的事物更相似,并且每个测量点都具有随距离而减小的局部影响。它为最靠近预测位置的点提供更大的权重,并且权重随距离的变化而减小。影响 IWD 精度的因素是功率参数和大小的值以及邻居的数量。
我们将使用 gstat 包使用 IDW 插值 SOC。首先,我们使用 krige() 函数拟合一个模型 (~ 1表示) “仅截取”。在空间数据的情况下,将仅使用 “x” 和 “y” 坐标。
1
2
IDW<- krige(SOC ~ 1, train, grid)
# [inverse distance weighted interpolation]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
summary(IDW)
# Object of class SpatialPixelsDataFrame
# Coordinates:
# min max
# x -1250285 119715
# y 998795 2538795
# Is projected: NA
# proj4string : [NA]
# Number of points: 10674
# Grid attributes:
# cellcentre.offset cellsize cells.dim
# x -1245285 10000 137
# y 1003795 10000 154
# Data attributes:
# var1.pred var1.var
# Min. : 0.4831 Min. : NA
# 1st Qu.: 4.2517 1st Qu.: NA
# Median : 5.7212 Median : NA
# Mean : 6.1423 Mean :NaN
# 3rd Qu.: 7.6260 3rd Qu.: NA
# Max. :29.0807 Max. : NA
# NA's :10674
转换为栅格
1
2
idw.na<-na.omit(idw)
IDW.pred<-rasterFromXYZ(as.data.frame(IDW)[, c("x", "y", "var1.pred")])
绘制 IDW 预测的 SOC
1
2
3
4
5
6
7
8
9
10
11
ggR(IDW.pred, geom_raster = TRUE) +
scale_fill_gradientn("SOC", colours = c("orange", "yellow", "green", "sky blue","blue"))+
theme_bw()+
theme(axis.title.x=element_blank(),
axis.text.x=element_blank(),
axis.ticks.x=element_blank(),
axis.title.y=element_blank(),
axis.text.y=element_blank(),
axis.ticks.y=element_blank())+
ggtitle("Inverse Distance Weighted (IDW)\n Predicted SOC")+
theme(plot.title = element_text(hjust = 0.5))
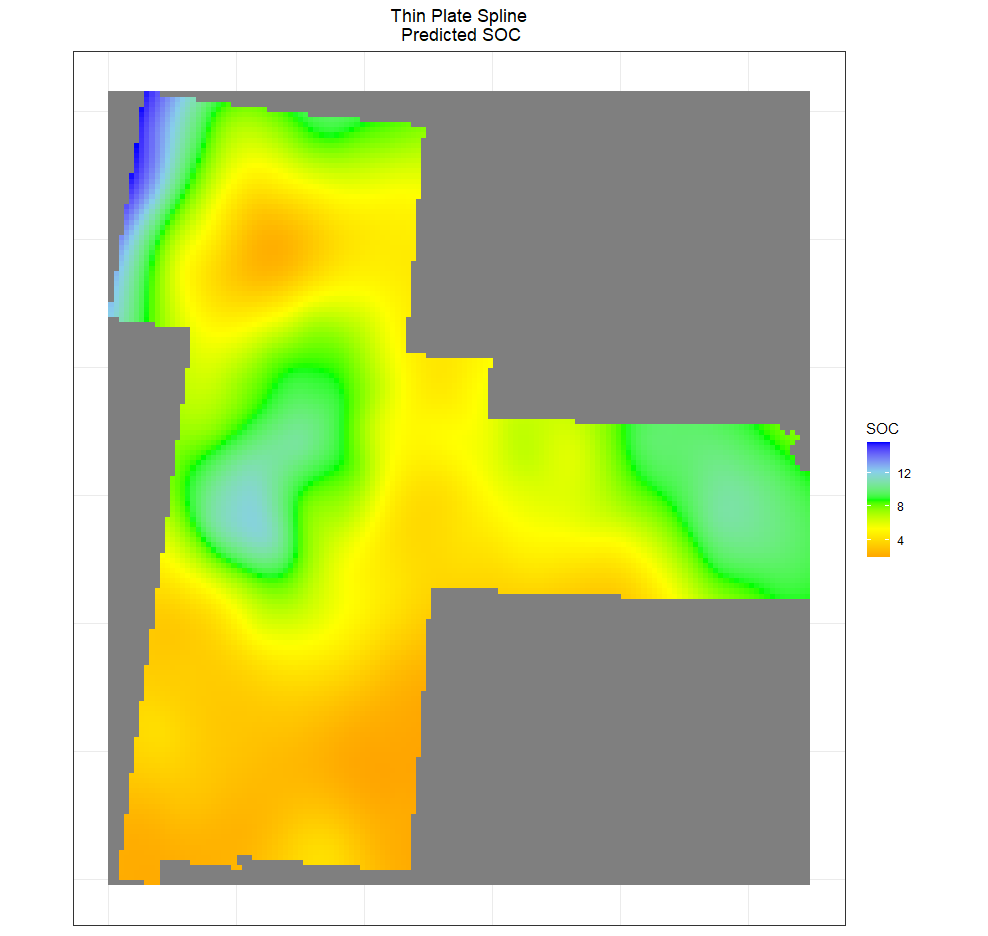
薄板样条插值
薄板样条用于在多个维度上产生对给定数据的近似值。这些类似于一维的三次样条。我们可以将薄板样条曲面拟合到不规则间隔的空间数据。
我们使用 field 包的 Tps() 函数创建薄板样条曲面。
1
2
3
m <- Tps(coordinates(train), train$SOC)
tps <- interpolate(r, m)
plot(tps)
1
tps <- raster::mask(tps,bd) # mask out
1
2
3
4
5
6
7
8
9
10
11
ggR(tps, geom_raster = TRUE) +
scale_fill_gradientn("SOC", colours = c("orange", "yellow", "green", "sky blue","blue"))+
theme_bw()+
theme(axis.title.x=element_blank(),
axis.text.x=element_blank(),
axis.ticks.x=element_blank(),
axis.title.y=element_blank(),
axis.text.y=element_blank(),
axis.ticks.y=element_blank())+
ggtitle("Thin Plate Spline\n Predicted SOC")+
theme(plot.title = element_text(hjust = 0.5))
地统计学插值
使用地统计学技术进行空间插值已广泛用于绘制环境变量。地统计学依赖于随机函数的概念,其中未知值的集合被视为一组空间依赖的随机变量。随机函数概念允许考虑属性空间变化中的结构。与确定性插值方法不同,地统计学假定域中的所有值都是具有依赖性的随机过程的结果。在任何特定位置,属性值的不确定性是根据该位置的随机变量的一组可能结果来估计的。这样,我们就可以对整个研究区域的空间预测的不确定性进行建模。
地统计插值模型涉及的主要步骤是:
- 检查数据 (分布、趋势、方向分量、异常值)。
- 计算经验半变异函数或协方差值。
- 将模型拟合到经验值。
- 生成克里金方程的矩阵。
- 对它们进行求解,以获得预测值以及与之相关的输出表面中每个位置的误差 (不确定性)。
地统计学广泛应用于科学和工程的许多领域,例如:
- 量化矿业矿产资源
- 环境科学中的污染制图和风险评估
- 土壤变量的数字制图
- 气象应用中温度、降雨量和相关变量 (如酸雨) 的预测
- 在公共卫生领域
半变异函数建模
半变异函数是描述空间随机变量的空间相关程度的函数。在空间建模中,半变异函数以经验半变异函数的图开始,它是间隔一段距离的点之间的平均平方差的一半。半变异函数的计算公式为:
半变异函数与协方差函数直接相关,协方差函数测量统计相关性或相似性作为距离的函数的强度。与协方差函数函数不同,实验半变异函数测量以矢量h (滞后距离) 分隔的数据之间的平均差异。计算平均半变异函数的成对之间的距离称为滞后。
在本练习中,我们将介绍:
- 实验变差函数
- 方差图云
- 各向同性变差函数
- 各向异性方差图
- 拟合变异函数模型
- 拟合优度
- 转换数据的变异函数建模
- 嵌套模型拟合
加载包和数据
1
2
3
4
5
6
7
library(gstat)
library(moments)
library(raster)
# Define data folder
dataFolder<-"D:\\Env\\DATA_08\\"
train<-read.csv(paste0(dataFolder,"train_data.csv"), header= TRUE)
实验变异函数
我们使用 gstat 包的 variovariogram() 函数来计算 SOC 的实验变异函数。在此之前,我们必须将 x 和 y 变量定义为坐标。
1
coordinates(train) = ~x+y
变异函数云图
我们将使用所有默认值来计算半方差云,该云显示数据集内所有位置对的半方差图值,并将它们绘制为分隔两个位置的距离的函数。
1
2
3
4
5
6
7
8
9
v.cloud<-variogram(SOC~ 1, data = train, cloud=T)
head(v.cloud)
# dist gamma dir.hor dir.ver id left right
# 1 511201.3 16.1425620 0 0 var1 2 1
# 2 430399.9 35.7266045 0 0 var1 3 1
# 3 186259.2 3.8392205 0 0 var1 3 2
# 4 256816.3 17.7786845 0 0 var1 4 1
# 5 287418.1 0.0394805 0 0 var1 4 2
# 6 294316.2 3.1000500 0 0 var1 4 3
1
plot(v.cloud, main = "Variogram cloud", xlab = "Separation distance (m)")
变异函数云显示了所有的点对,但很难检验空间相关性的一般模式。为了检查空间相关性,我们将计算经验变异函数,它将云组织成箱,就像直方图一样。
各向同性变异函数
当空间依赖性在所有方向上都相同时。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
v<-variogram(SOC~ 1, data = train, cloud=F)
v
# np dist gamma dir.hor dir.ver id
# 1 342 31257.18 17.37406 0 0 var1
# 2 1103 68803.65 19.87922 0 0 var1
# 3 1641 112768.06 21.46750 0 0 var1
# 4 2168 156934.71 23.24128 0 0 var1
# 5 2481 201237.11 22.90060 0 0 var1
# 6 2757 245847.81 25.82815 0 0 var1
# 7 2903 290428.32 26.94507 0 0 var1
# 8 2959 335388.48 25.33999 0 0 var1
# 9 3157 379593.68 26.05625 0 0 var1
# 10 3197 424435.66 25.78618 0 0 var1
# 11 3147 469107.57 27.48611 0 0 var1
# 12 3251 513418.76 27.54411 0 0 var1
# 13 3140 558052.44 26.53490 0 0 var1
# 14 3043 603268.68 27.46021 0 0 var1
# 15 2976 647329.04 26.89069 0 0 var1
1
plot(v, main = "Variogram - default", xlab = "Separation distance (m)")
我们可以将 cutoff (最大间隔) 设置为用 cutoff 可选参数指定,将 bin width 与 width 可选参数指定为 variogram 方法。
cutoff: 半方差估计中包含点对的空间间隔距离; 默认情况下,数据框对角线的长度除以3。。
width: 是数据点对被分组用于半方差估计的后续距离间隔
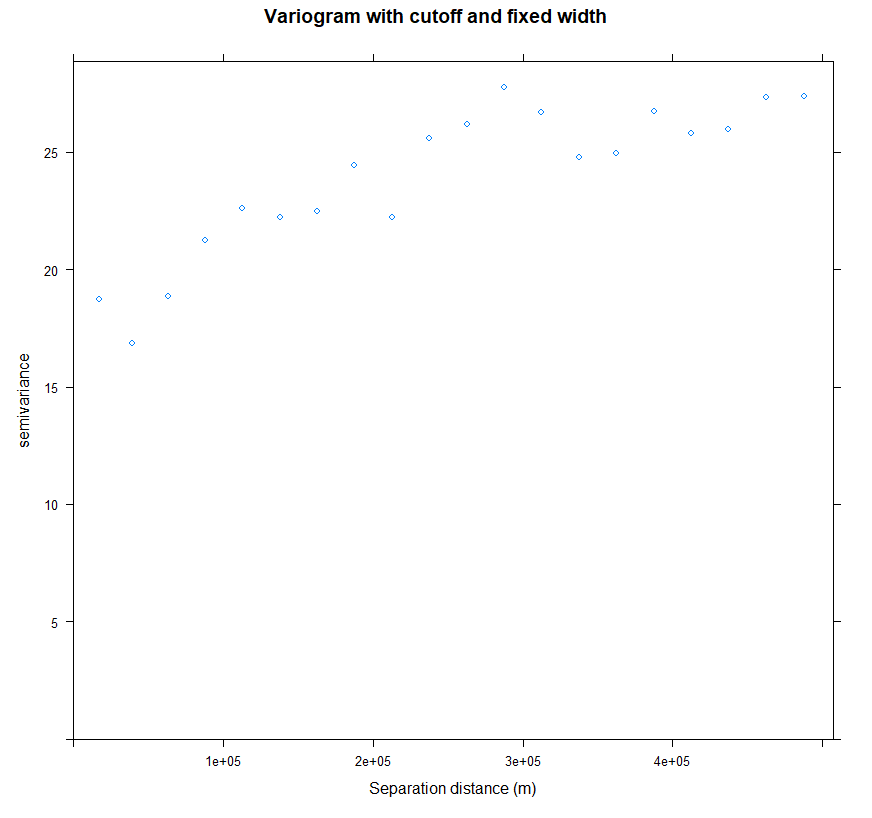
让我们尝试计算具有 500Km cutoff 和 2500 width 的半变异函数:
1
2
v.cut<-variogram(SOC ~ 1, train, cutoff=500000, width=500000/20)
plot(v.cut, main = "Variogram with cutoff and fixed width", xlab = "Separation distance (m)")
各向异性变异函数
当空间依赖性 (自相关) 在一个方向上比在其他方向更强时。我们可以通过变异函数曲面 (也称为 “变异函数图”) 和方向变异函数的可视化来检测各向异性。
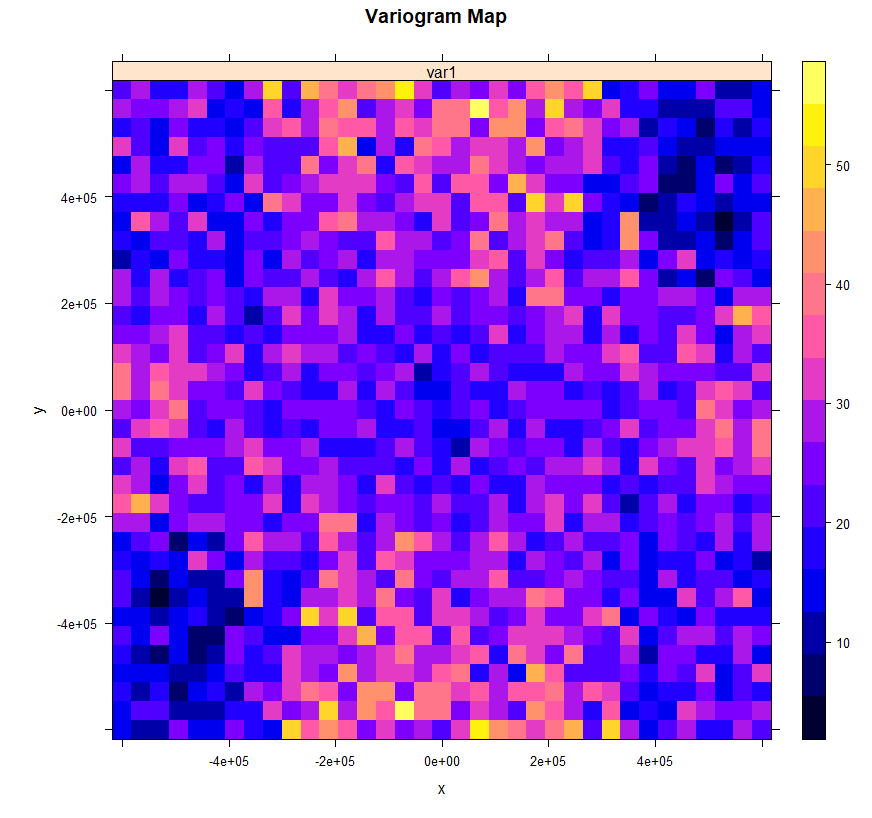
变异函数图
我们将使用带有可选参数 map=TRUE 的变异函数方法:
1
2
3
4
5
v.map<-variogram(SOC ~ 1, train, map = TRUE, cutoff=600000, width=600000/17)
plot(v.map, col.regions = bpy.colors(64),
main="Variogram Map",
xlab="x",
ylab="y")
方向变异函数
现在,显示 30°N 和 120°N 处 SOC 含量的方向变异函数,即各向异性椭圆的疑似长轴和小轴。
1
2
3
4
5
6
plot(variogram(SOC ~ 1, train,
alpha = c(30, 120),
cutoff = 600000),
main = "Directional Variograms, SOC",
sub = "Azimuth 30N (left), 120N (right)",
pch = 20, col = "blue")
拟合变异函数模型
计算出实验变异函数后,我们通常会在变异函数图中观察半变异函数,然后选择合理的模型将半变异函数曲线拟合到经验数据中。根据最小方差估计原理,采用最小二乘法拟合变异函数。目标是实现最佳拟合,并在模型中纳入我们对现象的了解。然后,模型参数将用于克里金法预测。
可以从拟合模型中计算出多个参数。半变异函数在变平时达到的高度或模型首次变平的值称为窗台。它通常由两个部分组成: 金块和部分门槛。原点处的不连续性或半变异函数 (几乎) 截取y值的值,称为金块效应。金块效应解释了测量误差和微观尺度变化。门槛首先变平的距离是呼叫范围。在 gstat 模型中,门槛被指定为部分门槛,即总门槛和掘金之间的差值。这也称为结构门槛。
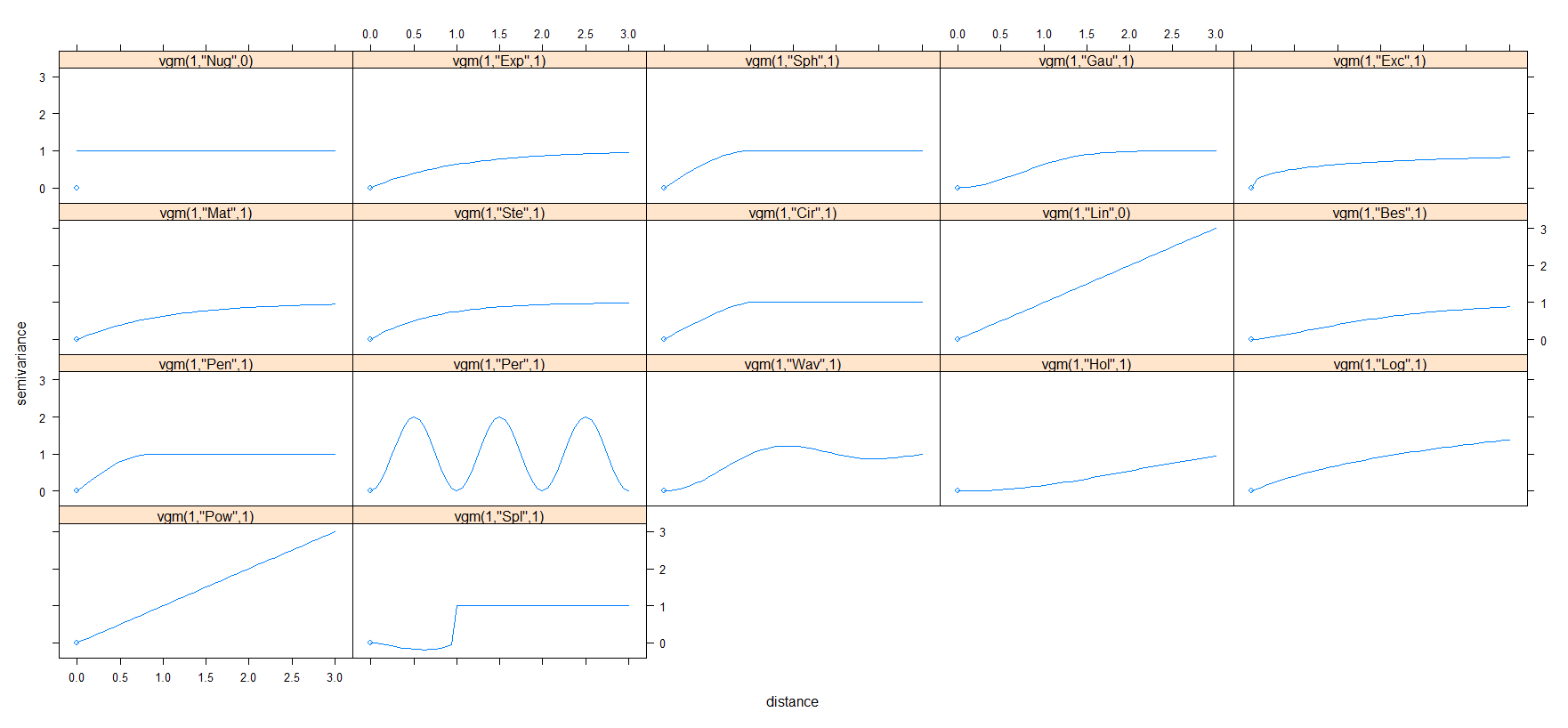
在 gstat 包中有几个模型可用于拟合变异函数。我们可以使用 show.vgms() 函数查看 gstat 中所有模型的形式。
1
show.vgms()
最常见的变异函数模型主要有线性模型、球形模型、指数模型和高斯模型等。这些模型的数学表达式如下:
首先,我们将使用 vgm() 方法创建变异函数模型对象,通过目测设置 range、sill 和 nugget 值来拟合初始模型,然后使用 fit.variogram() 函数自动调整参数。我们将用 Exp(指数) 和 Sph(球形) 来拟合模型。
指数 (Exp) 模型
1
2
3
4
5
6
7
8
# 目测设置初始参数
m.exp<-vgm(25,"Exp",25000,10)
# least square fit
m.exp.f<-fit.variogram(v, m.exp)
m.exp.f
# model psill range
# 1 Nug 15.12586 0.0
# 2 Exp 12.20305 148458.6
1
2
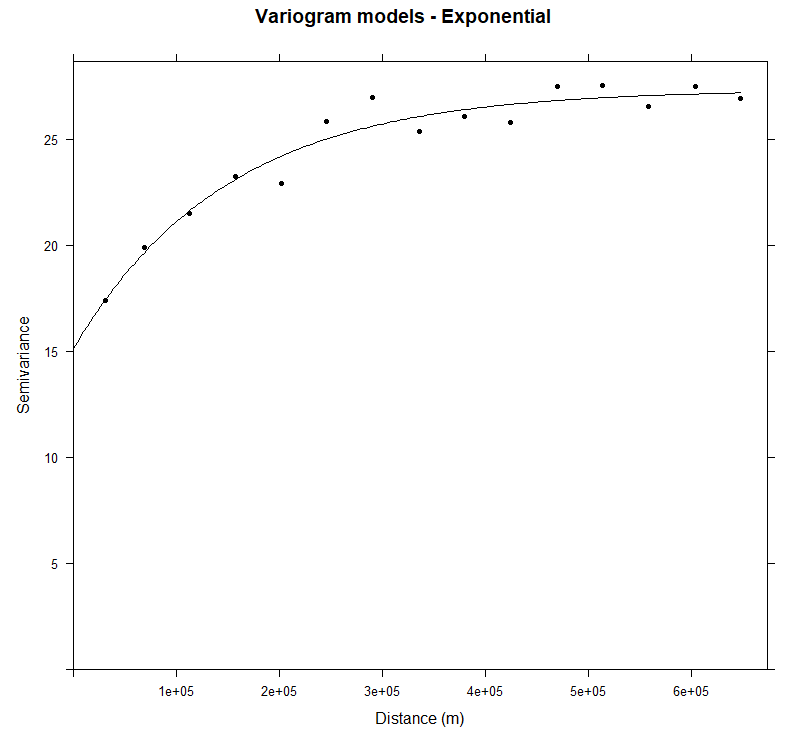
plot(v, pl=F, model=m.exp.f,col="black", cex=1, lwd=0.5,lty=1,pch=20,
main="Variogram models - Exponential",xlab="Distance (m)",ylab="Semivariance")
上图显示了土壤 SOC 的实验变异函数和拟合模型。SOC 的变异函数显示出明显的空间依赖性与有界的sill,并且与指数模型非常吻合。SOC 的方差随着滞后距离的增加而稳定地增加,并且在 148458.6m 的范围内慢慢的接近其门槛,并且自相关可以扩展到 3X148458.6m 的有效范围 (在指数模型中是范围的3倍)。
球面(Sph)模型
1
2
3
4
5
6
7
8
# Intial parameter set by eye esitmation
m.sph<-vgm(25,"Sph",40000,10)
# least square fit
m.sph.f<-fit.variogram(v, m.sph)
m.sph.f
# model psill range
# 1 Nug 9.170219 0.00
# 2 Sph 13.482728 55366.02
1
2
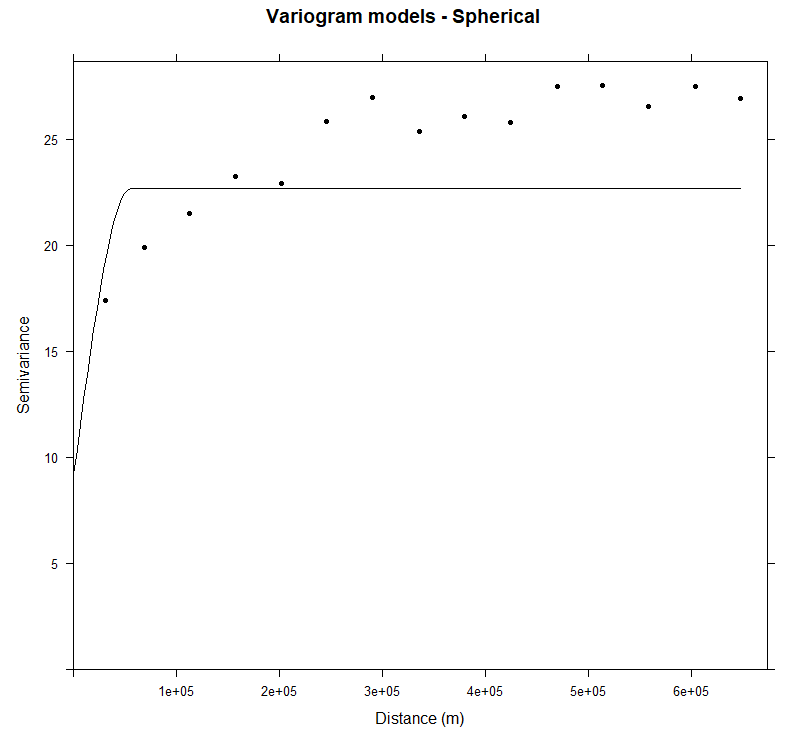
plot(v, pl=F, model=m.sph.f,col="black", cex=1, lwd=0.5,lty=1,pch=20,
main="Variogram models - Spherical",xlab="Distance (m)",ylab="Semivariance")
在 324339.6m 范围内,SOC 的变差函数与球形模型拟合较好,且边界层比指数模型更有界。
拟合优度
现在我们将量化变异函数模型与经验变异函数的拟合程度(内部拟合优度)。这是从模型拟合中加权的残差平方和。当然,越低越好。
1
2
attributes(m.exp.f)$SSErr
# [1] 2.561876e-07
1
2
attributes(m.sph.f)$SSErr
# [1] 6.223063e-06
我们可以用一组模型拟合实验变异函数,在这种情况下,将返回最佳拟合:
1
2
3
4
fit.variogram(v, vgm(c("Exp", "Sph", "Mat")))
# model psill range
# 1 Nug 15.12586 0.0
# 2 Exp 12.20305 148458.6
用变换后的数据进行变异函数建模
克里金法的关键假设是平稳性的正确形式 (二阶,内在),而不是概率分布。但是,如果数据的经验分布偏斜,则 kriging 估计量对一些大数据值敏感。让我们检查 SOC 的分布和偏度。
我们应用 moments 包中的函数 skewness() 来计算 SOC 的偏态系数。
1
2
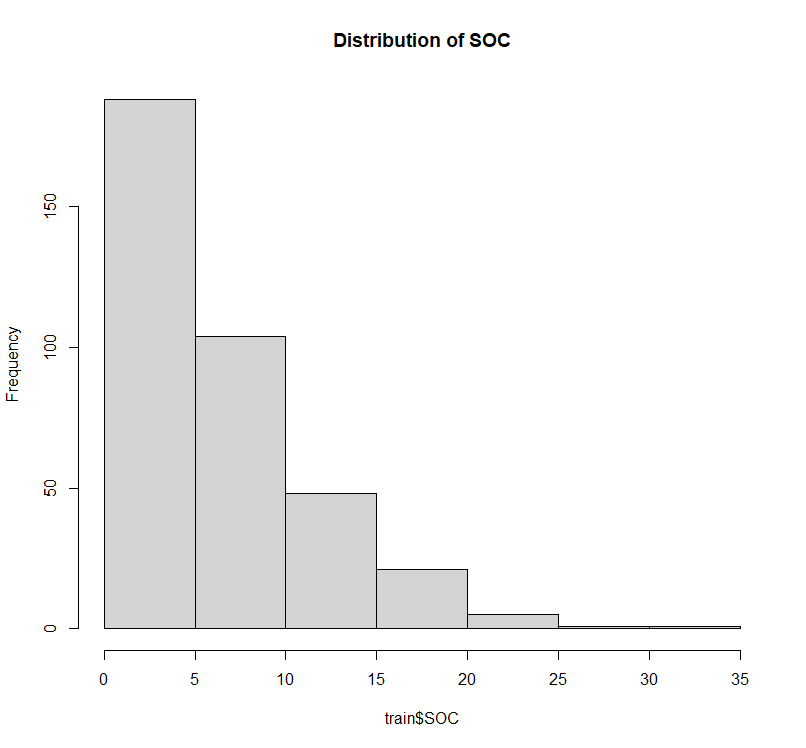
hist(train$SOC,
main= "Distribution of SOC")
1
2
skewness(train$SOC)
# [1] 1.412073
所以SOC数据高度正偏 (偏度 > 1)
R 函数 shapiro.test() 可用于对一个变量 (单变量) 进行正态性的 Shapiro-Wilk 检验:
1
2
3
4
shapiro.test(train$SOC)
# Shapiro-Wilk normality test
# data: train$SOC
# W = 0.88057, p-value = 2.7e-16
根据上述输出,p 值 < 0.05 意味着 SOC 的分布与正态分布显著不同。换句话说,我们可以假设 SOC 不是正态分布的。
因此,SOC 值高度偏斜且非正态分布,最好使用转换后的数据进行地统计建模。我们可以在 R (http://rcompanion.org/handbook/I_12.html) 中以不同的方式转换数据。在这里,我们尝试 log10 和幂变换。
Log10转换
1
2
train$logSOC<-log10(train$SOC)
hist(train$logSOC, main="Log10 transformed SOC")
1
2
3
4
5
6
skewness(train$logSOC)
# [1] -0.6221917
shapiro.test(train$logSOC)
# Shapiro-Wilk normality test
# data: train$logSOC
# W = 0.97465, p-value = 4.743e-06
幂变换 (Box-Cox)
幂变换使用 Box和Cox (1964) 的最大似然方法来选择针对正态性的单变量或多变量响应的变换。首先,我们必须使用 car 包的 powerTransform() 函数计算适当的转换参数,然后使用此参数使用 bcPower() 函数对数据进行转换。
1
2
3
4
5
6
7
8
9
10
library(car)
powerTransform(train$SOC)
# Estimated transformation parameter
# train$SOC
# 0.2523339
train$SOC.bc<-bcPower(train$SOC, 0.2523339)
hist(train$SOC.bc,
main="Box-Cox Transformation of SOC")
1
2
3
4
5
6
skewness(train$SOC.bc)
# [1] -0.03190983
shapiro.test(train$SOC.bc)
# Shapiro-Wilk normality test
# data: train$SOC.bc
# W = 0.99625, p-value = 0.5407
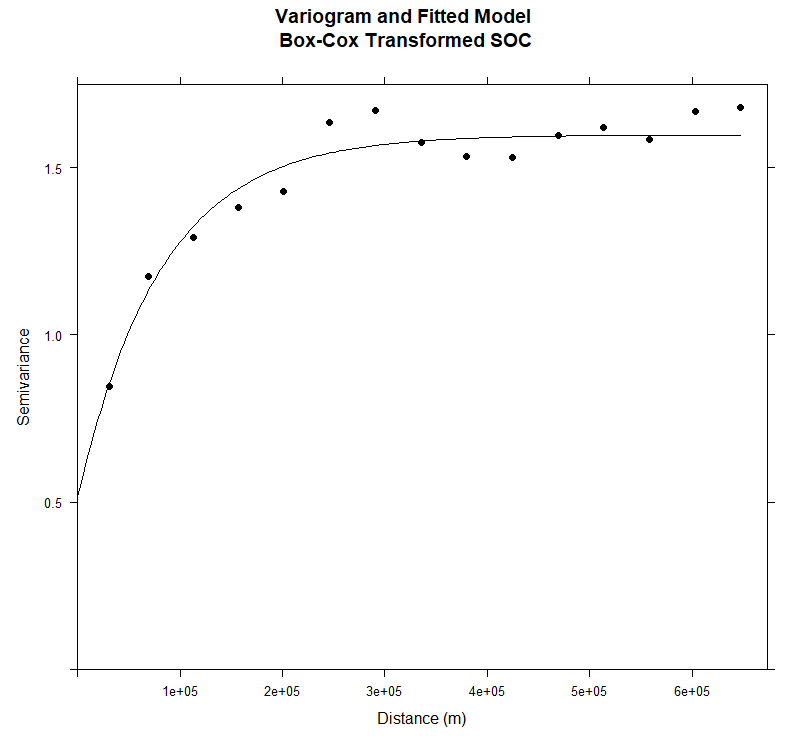
幂变换后的 SOC 完全正态分布,偏度接近于零。因此,我们将对转换后的 SOC 进行进一步分析。让我们用幂变换数据拟合变异函数模型:
1
2
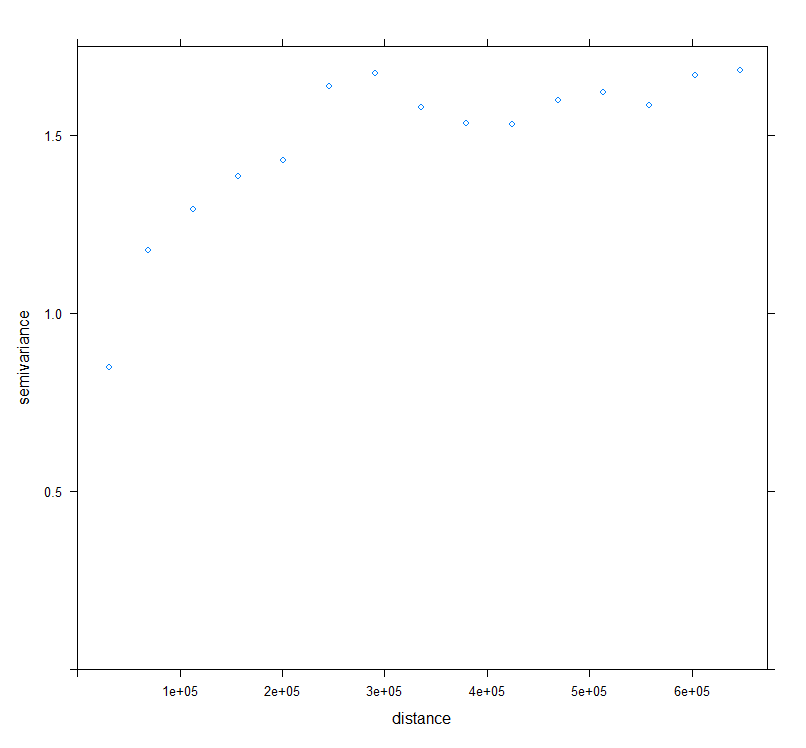
v.bc<-variogram(SOC.bc~ 1, data = train, cloud=F)
plot(v.bc)
1
2
3
4
# Intial parameter set by eye esitmation
m.bc<-vgm(1.5,"Exp",40000,0.5) # Exponential model
# least square fit
m.f.bc<-fit.variogram(v.bc, m.bc)
1
2
3
4
5
6
7
8
9
10
11
#### Plot varigram and fitted model:
plot(v.bc, pl=F,
model=m.f.bc,
col="black",
cex=0.9,
lwd=0.5,
lty=1,
pch=19,
main="Variogram and Fitted Model\n Box-Cox Transformed SOC",
xlab="Distance (m)",
ylab="Semivariance")
嵌套模型拟合
当您尝试通过拟合理论模型来表示经验半变异函数时,您可能会发现使用理论模型的组合会比使用单个模型更准确地拟合经验半变异函数。这就是所谓的模型嵌套。作为两个或多个半方差结构之和的半方差模型称为嵌套模型。
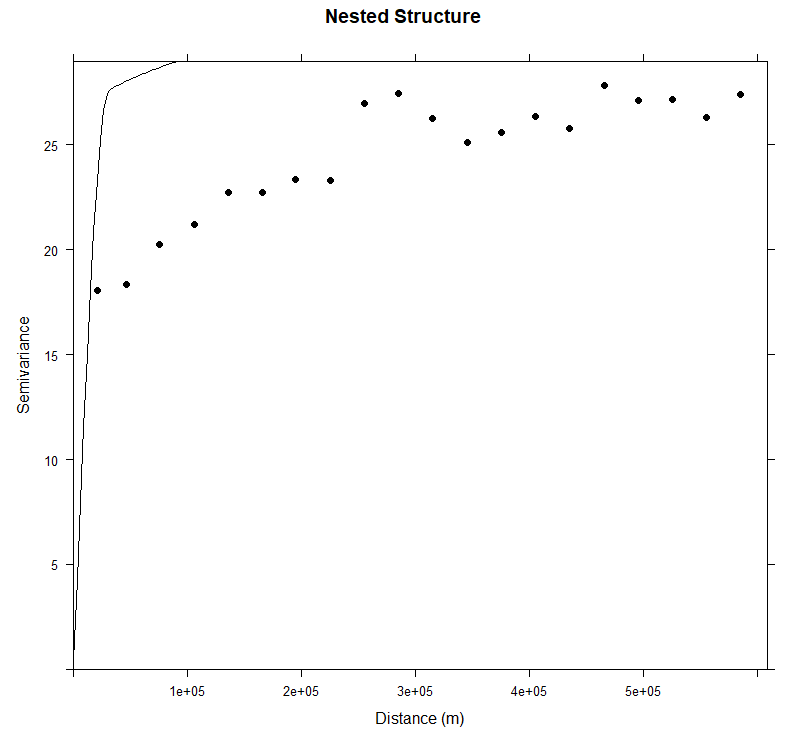
现在,我们将对具有两个结构成分的经验变异函数进行建模: 具有 sherical 模型的短程结构和长程结构。
短程结构
1
2
3
4
5
v<-variogram(SOC~ 1, data = train, cloud=F, cutoff=600000, width=600000/20)
(vm <- vgm(20, "Sph", 45000, 10))
# model psill range
# 1 Nug 10 0
# 2 Sph 20 45000
1
2
3
vmf <- fit.variogram(v, vm)
# Warning message:
# In fit.variogram(v, vm) : singular model in variogram fit
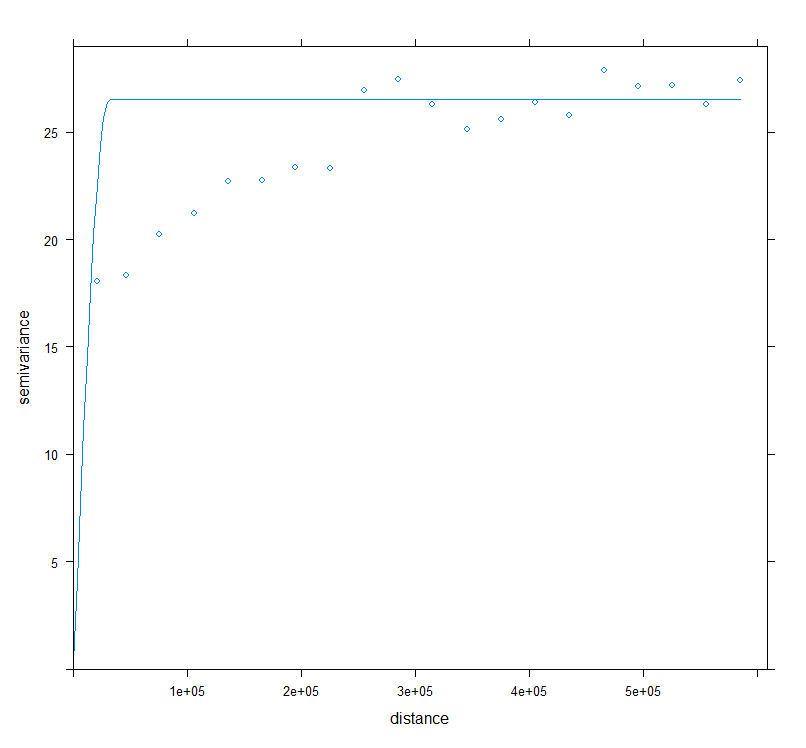
1
plot(v,model=vmf)
远程结构
1
2
3
4
5
(vm <- vgm(4, "Exp", 95000, add.to = vmf))
# model psill range
# 1 Nug 0.4117258 0.00
# 2 Sph 26.0896470 31112.87
# 3 Exp 4.0000000 95000.00
1
2
3
(vmf2 <- fit.variogram(v, vm))
# Warning message:
# In fit.variogram(v, vm) : singular model in variogram fit
1
2
3
4
5
6
7
8
9
10
11
#### Plot varigram and fitted model:
plot(v, pl=F,
model=vmf2,
col="black",
cex=0.9,
lwd=0.5,
lty=1,
pch=19,
main="Nested Structure",
xlab="Distance (m)",
ylab="Semivariance")