地统计学空间插值【R】

Posted Feb 20, 2023 Updated Oct 6, 2023

By renkaigis 89 min read

使用地统计学技术进行空间插值已广泛用于绘制环境变量。地统计学依赖于随机函数的概念，其中未知值的集合被视为一组空间依赖的随机变量。随机函数概念允许考虑属性空间变化中的结构。与确定性插值方法不同，地统计学假定域中的所有值都是具有依赖性的随机过程的结果。在任何特定位置，属性值的不确定性是根据该位置的随机变量的一组可能结果来估计的。这样，我们就可以对整个研究区域的空间预测的不确定性进行建模。

地统计插值模型涉及的主要步骤是:

检查数据 (分布、趋势、方向分量、异常值)。
计算经验半变异函数或协方差值。
将模型拟合到经验值。
生成克里金方程的矩阵。
对它们进行求解，以获得预测值以及与之相关的输出表面中每个位置的误差 (不确定性)。

地统计学广泛应用于科学和工程的许多领域，例如:

量化矿业矿产资源
环境科学中的污染制图和风险评估
土壤变量的数字制图
气象应用中温度、降雨量和相关变量 (如酸雨) 的预测
在公共卫生领域

原文链接：Geospatial Data Science with R

全部机翻，如有错误，以你的感觉为准。

半变异函数建模

半变异函数是描述空间随机变量的空间相关程度的函数。在空间建模中，半变异函数以经验半变异函数的图开始，它是间隔一段距离的点之间的平均平方差的一半。半变异函数的计算公式为:

半变异函数与协方差函数直接相关，协方差函数测量统计相关性或相似性作为距离的函数的强度。与协方差函数函数不同，实验半变异函数测量以矢量h (滞后距离) 分隔的数据之间的平均差异。计算平均半变异函数的成对之间的距离称为滞后。

在本练习中，我们将介绍:

实验变差函数
方差图云
各向同性变差函数
各向异性方差图
拟合变异函数模型
拟合优度
转换数据的变异函数建模
嵌套模型拟合

加载包和数据

  
library(gstat)
library(moments)
library(raster)

# Define data folder
dataFolder<-"D:\\Env\\DATA_08\\"
train<-read.csv(paste0(dataFolder,"train_data.csv"), header= TRUE) 

实验变异函数

我们使用 gstat 包的 variovariogram() 函数来计算 SOC 的实验变异函数。在此之前，我们必须将 x 和 y 变量定义为坐标。

  
coordinates(train) = ~x+y

变异函数云图

我们将使用所有默认值来计算半方差云，该云显示数据集内所有位置对的半方差图值，并将它们绘制为分隔两个位置的距离的函数。

  
v.cloud<-variogram(SOC~ 1, data = train, cloud=T)
head(v.cloud)
#       dist      gamma dir.hor dir.ver   id left right
# 1 511201.3 16.1425620       0       0 var1    2     1
# 2 430399.9 35.7266045       0       0 var1    3     1
# 3 186259.2  3.8392205       0       0 var1    3     2
# 4 256816.3 17.7786845       0       0 var1    4     1
# 5 287418.1  0.0394805       0       0 var1    4     2
# 6 294316.2  3.1000500       0       0 var1    4     3

  
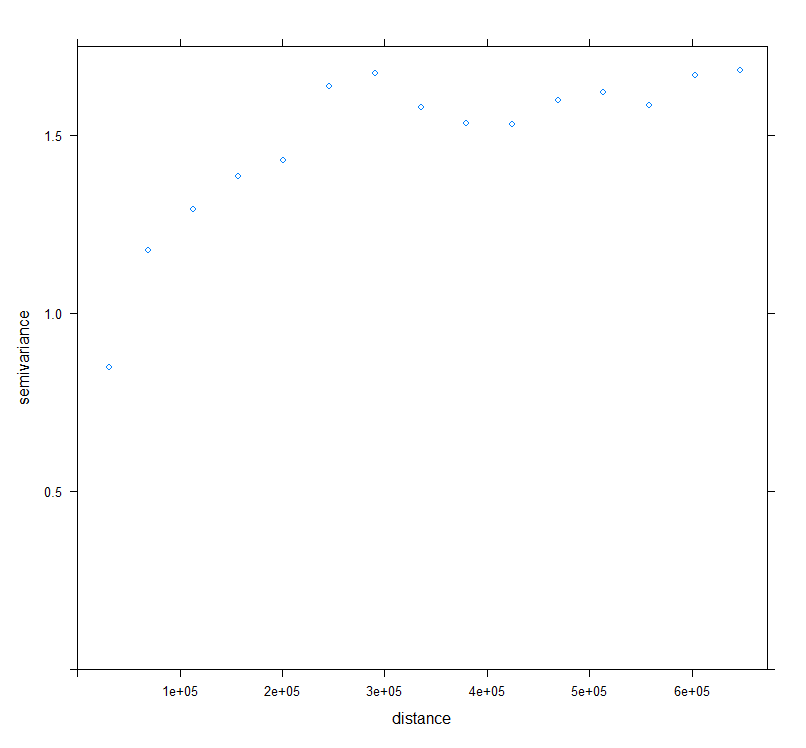
plot(v.cloud, main = "Variogram cloud", xlab = "Separation distance (m)")

变异函数云显示了所有的点对，但很难检验空间相关性的一般模式。为了检查空间相关性，我们将计算经验变异函数，它将云组织成箱，就像直方图一样。

各向同性变异函数

当空间依赖性在所有方向上都相同时。

  
v<-variogram(SOC~ 1, data = train, cloud=F)
v
#      np      dist    gamma dir.hor dir.ver   id
# 1   342  31257.18 17.37406       0       0 var1
# 2  1103  68803.65 19.87922       0       0 var1
# 3  1641 112768.06 21.46750       0       0 var1
# 4  2168 156934.71 23.24128       0       0 var1
# 5  2481 201237.11 22.90060       0       0 var1
# 6  2757 245847.81 25.82815       0       0 var1
# 7  2903 290428.32 26.94507       0       0 var1
# 8  2959 335388.48 25.33999       0       0 var1
# 9  3157 379593.68 26.05625       0       0 var1
# 10 3197 424435.66 25.78618       0       0 var1
# 11 3147 469107.57 27.48611       0       0 var1
# 12 3251 513418.76 27.54411       0       0 var1
# 13 3140 558052.44 26.53490       0       0 var1
# 14 3043 603268.68 27.46021       0       0 var1
# 15 2976 647329.04 26.89069       0       0 var1

  
plot(v, main = "Variogram - default", xlab = "Separation distance (m)")

我们可以将 cutoff (最大间隔) 设置为用 cutoff 可选参数指定，将 bin width 与 width 可选参数指定为 variogram 方法。

cutoff: 半方差估计中包含点对的空间间隔距离; 默认情况下，数据框对角线的长度除以3。。

width: 是数据点对被分组用于半方差估计的后续距离间隔

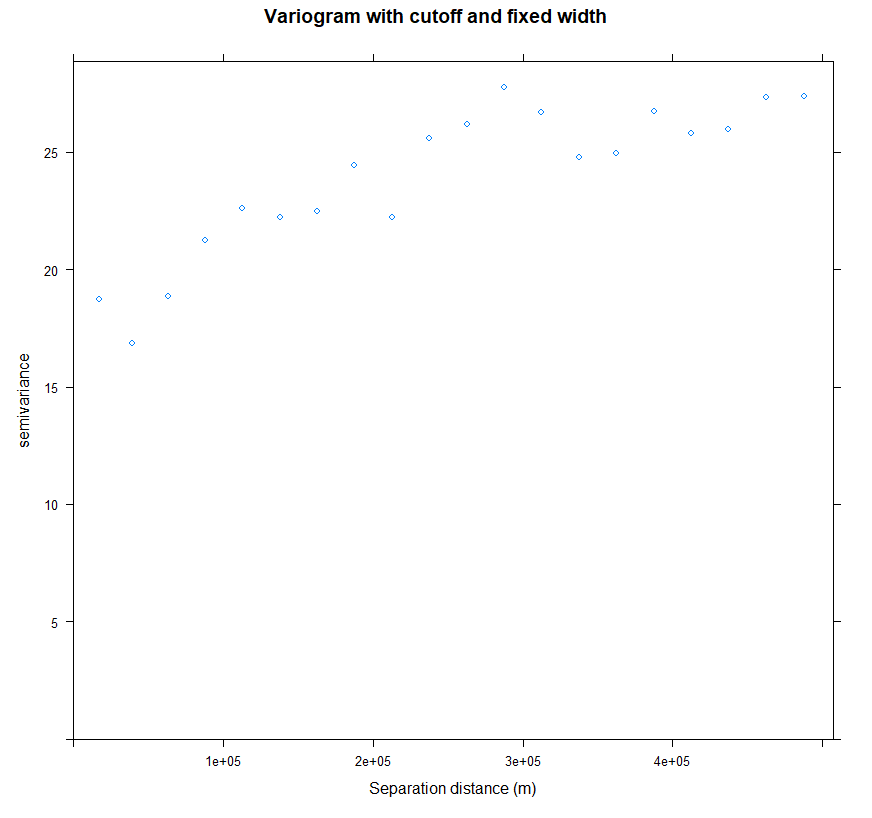
让我们尝试计算具有 500Km cutoff 和 2500 width 的半变异函数:

  
v.cut<-variogram(SOC ~ 1, train, cutoff=500000, width=500000/20)
plot(v.cut, main = "Variogram with cutoff and fixed width", xlab = "Separation distance (m)")

各向异性变异函数

当空间依赖性 (自相关) 在一个方向上比在其他方向更强时。我们可以通过变异函数曲面 (也称为 “变异函数图”) 和方向变异函数的可视化来检测各向异性。

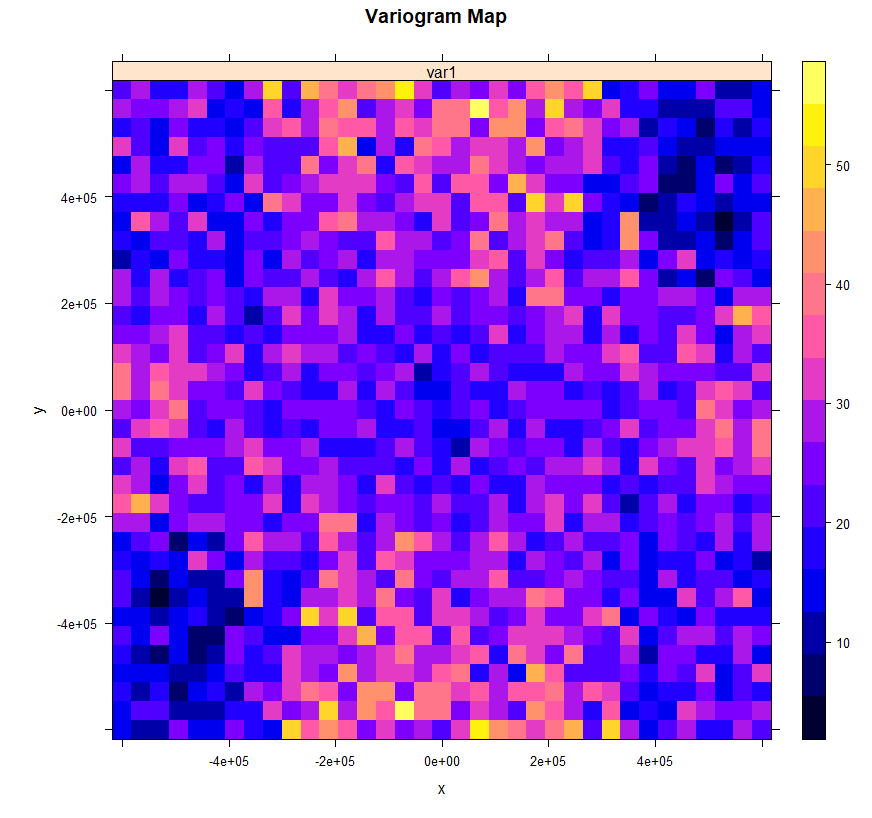
变异函数图

我们将使用带有可选参数 map=TRUE 的变异函数方法：

  
v.map<-variogram(SOC ~ 1, train, map = TRUE, cutoff=600000, width=600000/17)
plot(v.map, col.regions = bpy.colors(64),
     main="Variogram Map",
     xlab="x",
     ylab="y")

方向变异函数

现在，显示 30°N 和 120°N 处 SOC 含量的方向变异函数，即各向异性椭圆的疑似长轴和小轴。

  
plot(variogram(SOC ~ 1, train, 
               alpha = c(30, 120),
               cutoff = 600000),  
               main = "Directional Variograms, SOC",
               sub = "Azimuth 30N (left), 120N (right)", 
               pch = 20, col = "blue")

拟合变异函数模型

计算出实验变异函数后，我们通常会在变异函数图中观察半变异函数，然后选择合理的模型将半变异函数曲线拟合到经验数据中。根据最小方差估计原理，采用最小二乘法拟合变异函数。目标是实现最佳拟合，并在模型中纳入我们对现象的了解。然后，模型参数将用于克里金法预测。

可以从拟合模型中计算出多个参数。半变异函数在变平时达到的高度或模型首次变平的值称为窗台。它通常由两个部分组成: 金块和部分门槛。原点处的不连续性或半变异函数 (几乎) 截取y值的值，称为金块效应。金块效应解释了测量误差和微观尺度变化。门槛首先变平的距离是呼叫范围。在 gstat 模型中，门槛被指定为部分门槛，即总门槛和掘金之间的差值。这也称为结构门槛。

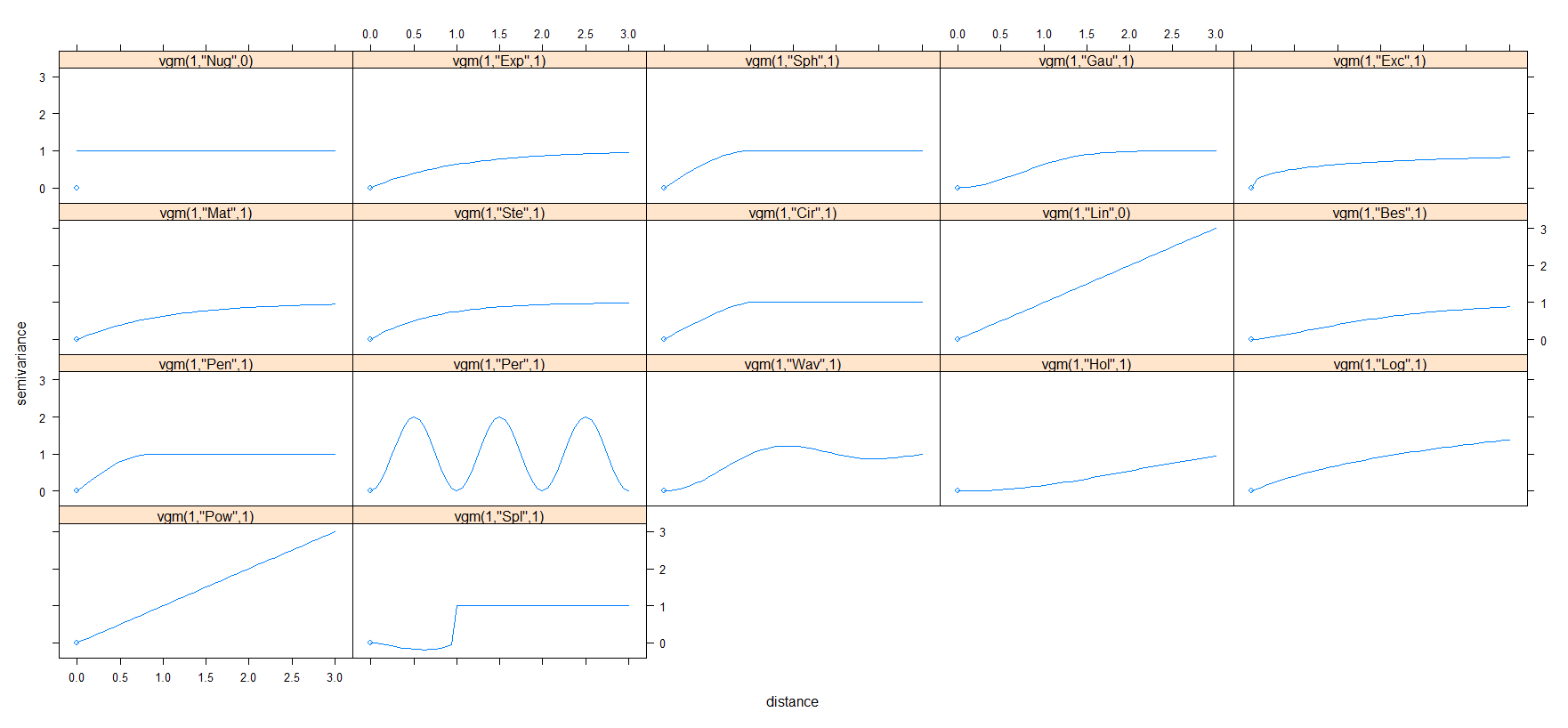
在 gstat 包中有几个模型可用于拟合变异函数。我们可以使用 show.vgms() 函数查看 gstat 中所有模型的形式。

  
show.vgms()

最常见的变异函数模型主要有线性模型、球形模型、指数模型和高斯模型等。这些模型的数学表达式如下:

首先，我们将使用 vgm() 方法创建变异函数模型对象，通过目测设置 range、sill 和 nugget 值来拟合初始模型，然后使用 fit.variogram() 函数自动调整参数。我们将用 Exp(指数) 和 Sph(球形) 来拟合模型。

指数 (Exp) 模型

  
# 目测设置初始参数
m.exp<-vgm(25,"Exp",25000,10)
# least square fit
m.exp.f<-fit.variogram(v, m.exp)
m.exp.f
#   model    psill    range
# 1   Nug 15.12586      0.0
# 2   Exp 12.20305 148458.6

  
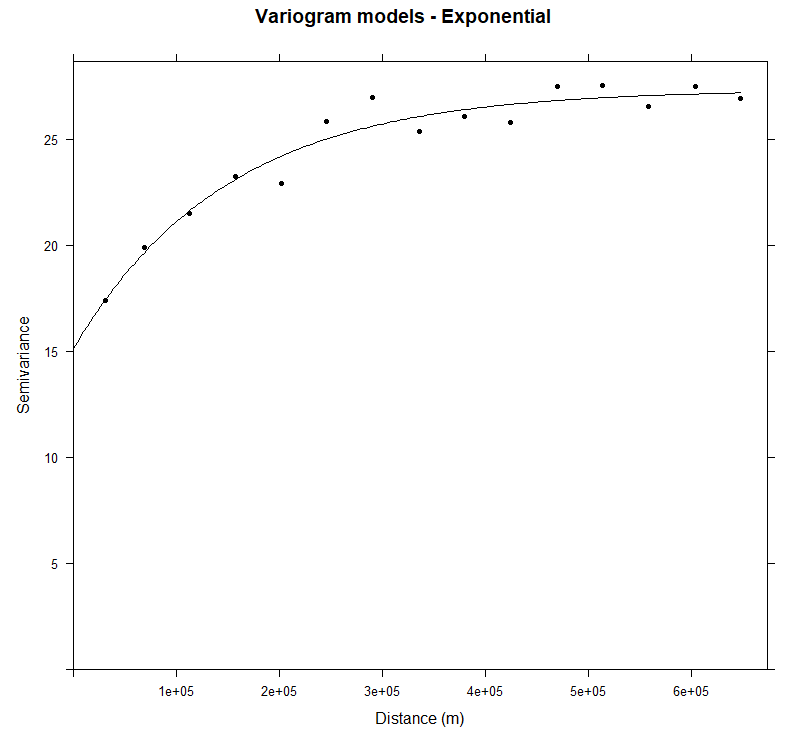
plot(v, pl=F, model=m.exp.f,col="black", cex=1, lwd=0.5,lty=1,pch=20,
     main="Variogram models - Exponential",xlab="Distance (m)",ylab="Semivariance")

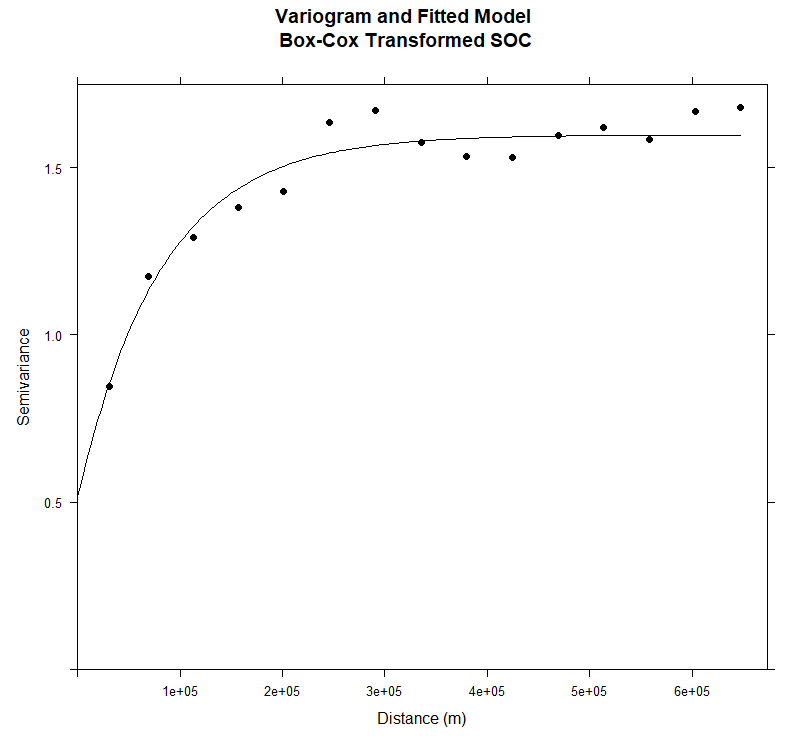
上图显示了土壤 SOC 的实验变异函数和拟合模型。SOC 的变异函数显示出明显的空间依赖性与有界的sill，并且与指数模型非常吻合。SOC 的方差随着滞后距离的增加而稳定地增加，并且在 148458.6m 的范围内慢慢的接近其门槛，并且自相关可以扩展到 3X148458.6m 的有效范围 (在指数模型中是范围的3倍)。

球面(Sph)模型

  
# Intial parameter set by eye esitmation
m.sph<-vgm(25,"Sph",40000,10)
# least square fit
m.sph.f<-fit.variogram(v, m.sph)
m.sph.f
#   model     psill    range
# 1   Nug  9.170219     0.00
# 2   Sph 13.482728 55366.02

  
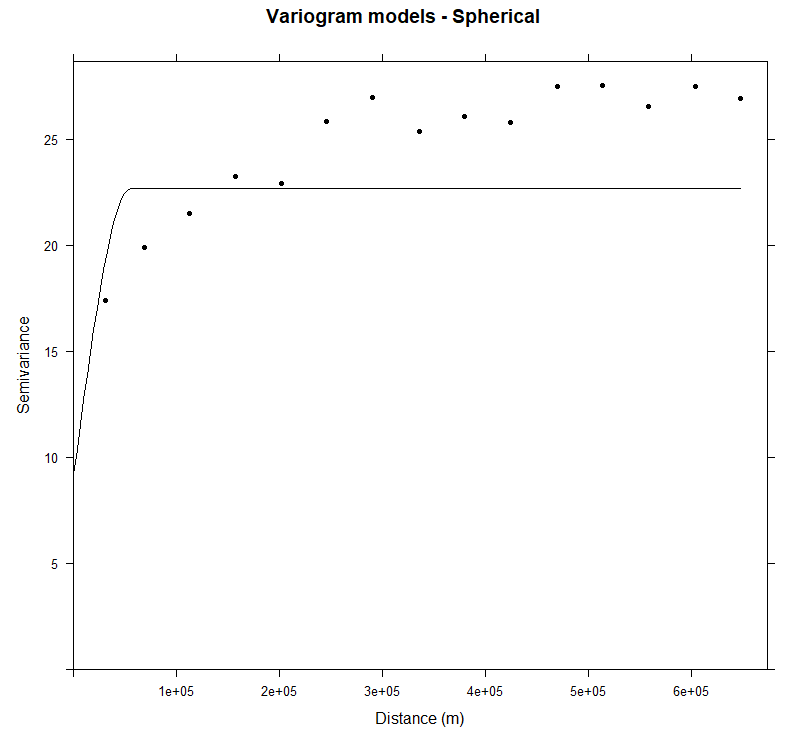
plot(v, pl=F, model=m.sph.f,col="black", cex=1, lwd=0.5,lty=1,pch=20,
     main="Variogram models - Spherical",xlab="Distance (m)",ylab="Semivariance")

在 324339.6m 范围内，SOC 的变差函数与球形模型拟合较好，且边界层比指数模型更有界。

拟合优度

现在我们将量化变异函数模型与经验变异函数的拟合程度(内部拟合优度)。这是从模型拟合中加权的残差平方和。当然，越低越好。

  
attributes(m.exp.f)$SSErr
# [1] 2.561876e-07

  
attributes(m.sph.f)$SSErr
# [1] 6.223063e-06

我们可以用一组模型拟合实验变异函数，在这种情况下，将返回最佳拟合:

  
fit.variogram(v, vgm(c("Exp", "Sph", "Mat")))
#   model    psill    range
# 1   Nug 15.12586      0.0
# 2   Exp 12.20305 148458.6

用变换后的数据进行变异函数建模

克里金法的关键假设是平稳性的正确形式 (二阶，内在)，而不是概率分布。但是，如果数据的经验分布偏斜，则 kriging 估计量对一些大数据值敏感。让我们检查 SOC 的分布和偏度。

我们应用 moments 包中的函数 skewness() 来计算 SOC 的偏态系数。

  
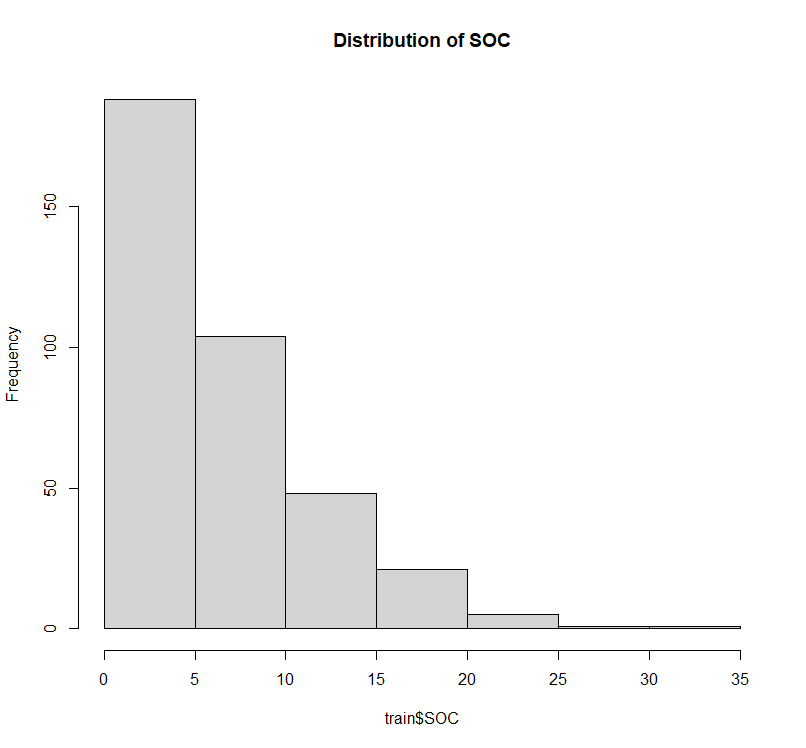
hist(train$SOC,
     main= "Distribution of SOC")

  
skewness(train$SOC) 
# [1] 1.412073

所以SOC数据高度正偏 (偏度 > 1)

R 函数 shapiro.test() 可用于对一个变量 (单变量) 进行正态性的 Shapiro-Wilk 检验:

  
shapiro.test(train$SOC)
# 	Shapiro-Wilk normality test
# data:  train$SOC
# W = 0.88057, p-value = 2.7e-16

根据上述输出，p 值 < 0.05 意味着 SOC 的分布与正态分布显著不同。换句话说，我们可以假设 SOC 不是正态分布的。

因此，SOC 值高度偏斜且非正态分布，最好使用转换后的数据进行地统计建模。我们可以在 R (http://rcompanion.org/handbook/I_12.html) 中以不同的方式转换数据。在这里，我们尝试 log10 和幂变换。

Log10转换

  
train$logSOC<-log10(train$SOC)
hist(train$logSOC, main="Log10 transformed SOC")

  
skewness(train$logSOC)
# [1] -0.6221917
shapiro.test(train$logSOC)
# 	Shapiro-Wilk normality test
# data:  train$logSOC
# W = 0.97465, p-value = 4.743e-06

幂变换 (Box-Cox)

幂变换使用 Box和Cox (1964) 的最大似然方法来选择针对正态性的单变量或多变量响应的变换。首先，我们必须使用 car 包的 powerTransform() 函数计算适当的转换参数，然后使用此参数使用 bcPower() 函数对数据进行转换。

  
library(car)
powerTransform(train$SOC)
# Estimated transformation parameter 
# train$SOC 
# 0.2523339 

train$SOC.bc<-bcPower(train$SOC, 0.2523339)

hist(train$SOC.bc,
     main="Box-Cox Transformation of SOC")

  
skewness(train$SOC.bc)
# [1] -0.03190983
shapiro.test(train$SOC.bc)
# 	Shapiro-Wilk normality test
# data:  train$SOC.bc
# W = 0.99625, p-value = 0.5407

幂变换后的 SOC 完全正态分布，偏度接近于零。因此，我们将对转换后的 SOC 进行进一步分析。让我们用幂变换数据拟合变异函数模型:

  
v.bc<-variogram(SOC.bc~ 1, data = train, cloud=F)
plot(v.bc)

  
# Intial parameter set by eye esitmation
m.bc<-vgm(1.5,"Exp",40000,0.5)  # Exponential model
# least square fit
m.f.bc<-fit.variogram(v.bc, m.bc)

  
#### Plot varigram and fitted model:
plot(v.bc, pl=F, 
     model=m.f.bc,
     col="black", 
     cex=0.9, 
     lwd=0.5,
     lty=1,
     pch=19,
     main="Variogram and Fitted Model\n Box-Cox Transformed SOC",
     xlab="Distance (m)",
     ylab="Semivariance")

嵌套模型拟合

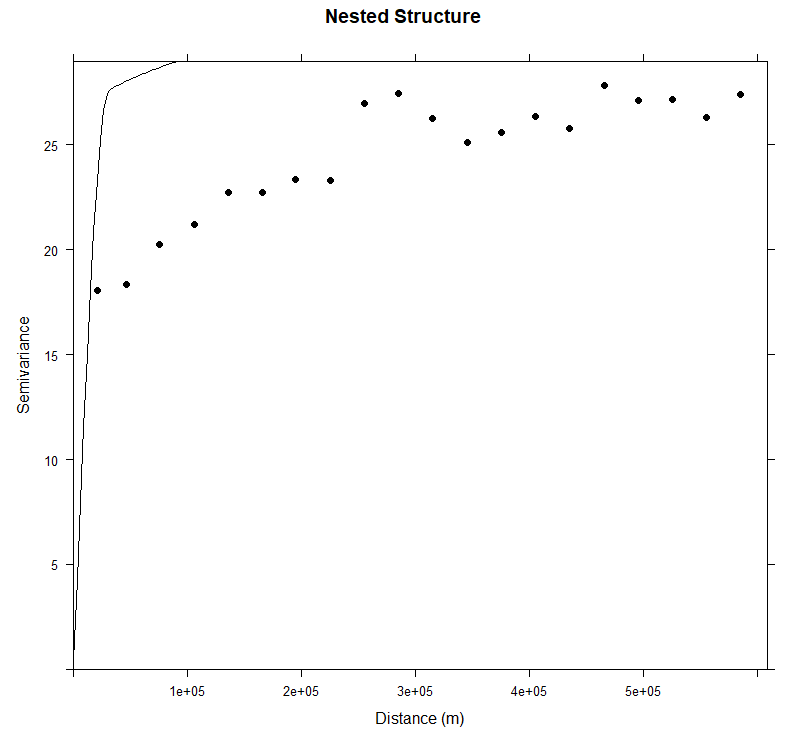
当您尝试通过拟合理论模型来表示经验半变异函数时，您可能会发现使用理论模型的组合会比使用单个模型更准确地拟合经验半变异函数。这就是所谓的模型嵌套。作为两个或多个半方差结构之和的半方差模型称为嵌套模型。

现在，我们将对具有两个结构成分的经验变异函数进行建模: 具有 sherical 模型的短程结构和长程结构。

短程结构

  
v<-variogram(SOC~ 1, data = train, cloud=F, cutoff=600000, width=600000/20)
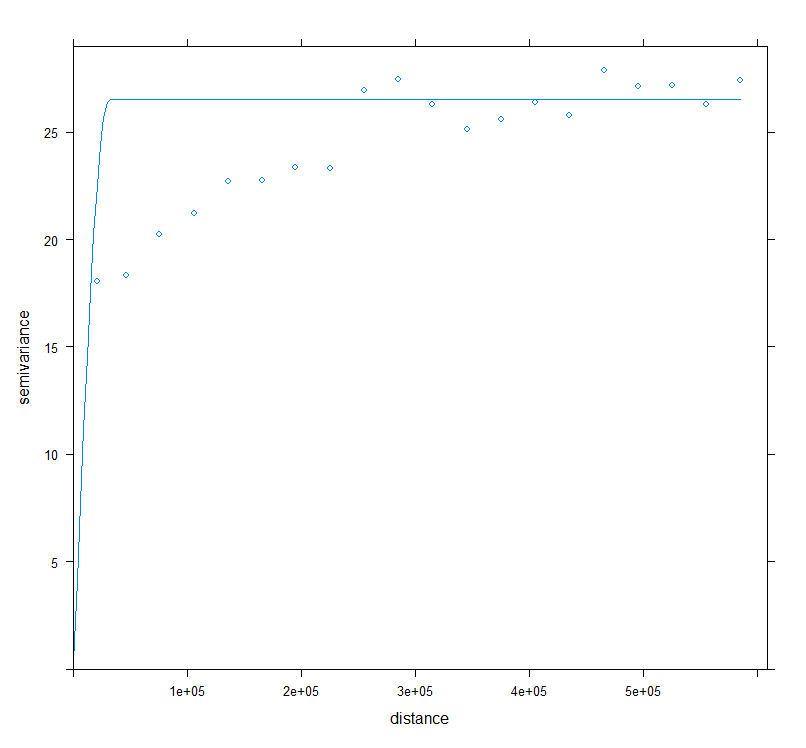
(vm <- vgm(20, "Sph", 45000, 10))
#   model psill range
# 1   Nug    10     0
# 2   Sph    20 45000

  
vmf <- fit.variogram(v, vm)
# Warning message:
# In fit.variogram(v, vm) : singular model in variogram fit

  
plot(v,model=vmf)

远程结构

  
(vm <- vgm(4, "Exp", 95000, add.to = vmf))
#   model      psill    range
# 1   Nug  0.4117258     0.00
# 2   Sph 26.0896470 31112.87
# 3   Exp  4.0000000 95000.00

  
(vmf2 <- fit.variogram(v, vm))
# Warning message:
# In fit.variogram(v, vm) : singular model in variogram fit

  
#### Plot varigram and fitted model:
plot(v, pl=F, 
     model=vmf2,
     col="black", 
     cex=0.9, 
     lwd=0.5,
     lty=1,
     pch=19,
     main="Nested Structure",
     xlab="Distance (m)",
     ylab="Semivariance")

克里金插值

克里金 (Kriging) 是一组地统计学技术，用于在未采样的位置从其在附近位置的值的已知观测值中插值随机场的值 (例如，作为地理位置的函数的土壤变量)。克里金法背后的主要统计假设是平稳性之一，这意味着统计属性 (例如均值和方差) 不取决于确切的空间位置，因此一个位置的变量的均值和方差等于均值和方差在另一个位置。克里金法的基本思想是通过计算点附近函数的已知值的加权平均值来预测给定点的值。与其他确定性插值方法 (例如反距离加权 (IDW) 和样条曲线) 不同，克里金法基于自相关-即，测量点之间的统计关系来插值空间场中的值。克里金法能够产生具有不确定性的预测面。尽管平稳性 (恒定均值和方差) 和各向同性 (所有方向的均匀性) 是kriging提供最佳线性无偏预测的两个主要假设，但是，对于各种形式和方法的kriging，这些假设具有灵活性。

克里金法的步骤：

搜索半径内样本的平均样本对样本变异性的计算；
选择位于搜索半径内的最近样本；
建立 kriging 矩阵，包括建立包含每个邻域样本值的预期样本变异性的半方差矩阵，以及建立包含每个最接近邻域样本值与块之间的平均变异性的矩阵；
克里金系数矩阵的建立; 以及
将克里金系数乘以它们各自的样本值，以提供克里金估计 (KE)。克里金方差 (KV) 是根据权重系数的乘积和它们各自的样本块方差计算得出的。一个额外的常数，滞后范围乘数被添加以最小化方差。

权重由基于数据空间结构的变异函数确定。这两个插补器的一般公式是数据的加权和:

克里金法的类型：

克里金法最常见的五种子类型，包括:

普通克里金法 (OK)

普通克里金法 (OK) 是应用最广泛的克里金法。这是一个线性无偏估计量，因为误差均值等于零。在 OK 中，通过强制 kriging 权重求和为1，从线性估计器中过滤局部均值。OK通常比简单的克里金法更可取，因为它既不需要知识，也不需要整个区域的均值平稳性

泛克里金法 (UK)

泛克里金法 (UK) 是普通克里金法在非平稳条件下的一种变体，在非平稳条件下，均值在不同位置 (局部趋势或漂移) 以确定性方式不同，而只有方差是恒定的。这种二阶平稳性 (“弱平稳性”) 通常是环境暴露的相关假设。在英国，通常首先将趋势作为坐标的函数进行计算，然后将随机场剩余的变化 (残差) 添加到趋势中以进行最终预测。

协同克里金 (CK)

协同克里金法 (CK) 是普通克里金法的扩展，其中使用了其他观察到的变量 (通常与感兴趣的变量相关的共同变量) 来提高感兴趣的变量的插值精度。与回归和通用克里金法不同，共克里金法不需要辅助信息在所有预测位置都可用。协变量可以在与目标 (共定位样本) 相同的点处、在其他点处或两者处测量。协克里金法最常见的应用是当协变量比目标变量更便宜的测量时。

回归克里金

回归 kriging (RK) 在数学上等效于通用 kriging 或带有外部漂移的 kriging，其中辅助预测器直接用于求解 kriging 权重。回归 kriging 将回归模型与回归残差的简单 kriging 相结合。首先计算并建模残差的实验变异函数，然后将简单的克里金法 (SK) 应用于残差，以给出残差的空间预测。

指示克里金

指示 kriging (IK) 是一种非参数地统计学方法，其中环境变量通过一组阈值 (例如，样本直方图的十进制，检测极限，监管阈值) 离散化变化范围，并将每个观察值转换为指标向量不超过每个阈值。然后，将 kriging 应用于指标集，并将估计值组合起来，形成条件累积分布函数 (ccdf)。概率分布的平均值或中位数可以用作污染物浓度的估计。指示 kriging 提供了一种灵活的插值方法，非常适合以下数据集: 1) 许多观测值低于检测极限，2) 直方图强烈偏斜，或3) 特定类别的属性值在空间中比其他属性值更好地连接 (例如，低污染物浓度) (Goovaerts，2009)。

OK，UK或RK插值方法可以以两种形式之一的准时/点或块应用。准时克里金法 (默认值) 估计给定点的值，并且最常用。块Kriging使用点周围给定位置 (例如 “块”) 的平均期望值的估计。块Kriging提供了更好的方差估计，并具有平滑插值结果的效果。

普通克里金

普通克里金法 (OK) 是应用最广泛的克里金法。这是一个线性无偏估计量，因为误差均值等于零。在OK中，通过强制kriging权重求和为1，从线性估计器中过滤局部均值。OK通常比简单的克里金法更可取，因为它既不需要知识，也不需要整个区域的均值平稳性。

我们将在本练习中介绍以下步骤:

数据变换
变异函数建模
点或准时克里金法
块克里金法

在克里金法之前，首先我们必须计算 SOC 的半变异函数并拟合模型。然后我们应用 gstat 包的 krige() 函数。

加载包和数据

土壤有机碳数据(训练和试验数据集)可以在这里找到。

  
library(plyr)
library(dplyr)
library(gstat)
library(raster)
library(ggplot2)
library(car)
library(classInt)
library(RStoolbox)
library(spatstat)
library(dismo)
library(fields)
library(gridExtra)

# Define data folder
dataFolder<-"D:\\Env\\DATA_08\\"

train<-read.csv(paste0(dataFolder,"train_data.csv"), header= TRUE) 
grid<-read.csv(paste0(dataFolder, "GP_prediction_grid_data.csv"), header= TRUE)

数据变换

幂变换使用 Box和Cox (1964) 的最大似然方法来选择针对正态性的单变量或多变量响应的变换。首先，我们必须使用 car 包的 powerTransform() 函数计算适当的转换参数，然后使用此参数使用 bcPower() 函数对数据进行转换。

  
powerTransform(train$SOC)
# Estimated transformation parameter 
# train$SOC 
# 0.2523339 

  
train$SOC.bc<-bcPower(train$SOC, 0.2523339)

定义x & y变量来坐标

  
coordinates(train) = ~x+y
coordinates(grid) = ~x+y

变异函数建模

  
# 变异函数
v<-variogram(SOC.bc~ 1, data = train, cloud=F)
# Intial parameter set by eye esitmation
m<-vgm(1.5,"Exp",40000,0.5)
# least square fit
m.f<-fit.variogram(v, m)
m.f
#   model     psill    range
# 1   Nug 0.5165678     0.00
# 2   Exp 1.0816886 82374.23

绘制变量图和拟合模型

  
#### Plot varigram and fitted model:
plot(v, pl=F, 
     model=m.f,
     col="black", 
     cex=0.9, 
     lwd=0.5,
     lty=1,
     pch=19,
     main="Variogram and Fitted Model\n Box-Cox Transformed SOC",
     xlab="Distance (m)",
     ylab="Semivariance")

点或准时克里金法

普通点克里金法是克里金法最简单的形式之一。通常，点克里金法使用克里金法从一组附近的样本值中估计点的值。

gstat 包中的 krige() 函数用于简单，普通或通用的kriging (有时称为外部漂移 kriging)，局部邻域中的 kriging，块平均值 (矩形或不规则块) 的点 kriging以及所有 kriging 变体的条件(高斯或指标)模拟等效，以及逆距离加权插值函数。，和反距离加权插值的函数。用于多变量预测。

  
OK<-krige(SOC.bc~1, 
              loc= train,        # Data frame
              newdata=grid,      # Prediction grid
              model = m.f)       # fitted varigram model
# [using ordinary kriging]

  
summary(OK)
# Object of class SpatialPointsDataFrame
# Coordinates:
#        min     max
# x -1245285  114715
# y  1003795 2533795
# Is projected: NA 
# proj4string : [NA]
# Number of points: 10674
# Data attributes:
#    var1.pred          var1.var     
#  Min.   :-0.1729   Min.   :0.7212  
#  1st Qu.: 1.3237   1st Qu.:0.9277  
#  Median : 1.8679   Median :1.0005  
#  Mean   : 1.8915   Mean   :1.0220  
#  3rd Qu.: 2.4842   3rd Qu.:1.0993  
#  Max.   : 4.1525   Max.   :1.4493  

逆变换

我们将使用使用过 Box-cos 变换的变换参数来逆变换。

  
k1<-1/0.2523339                                   
OK$OK.pred <-((OK$var1.pred *0.2523339+1)^k1)
OK$OK.var <-((OK$var1.var *0.2523339+1)^k1)
summary(OK)
# Object of class SpatialPointsDataFrame
# Coordinates:
#        min     max
# x -1245285  114715
# y  1003795 2533795
# Is projected: NA 
# proj4string : [NA]
# Number of points: 10674
# Data attributes:
#    var1.pred          var1.var         OK.pred           OK.var     
#  Min.   :-0.1729   Min.   :0.7212   Min.   : 0.838   Min.   :1.940  
#  1st Qu.: 1.3237   1st Qu.:0.9277   1st Qu.: 3.133   1st Qu.:2.302  
#  Median : 1.8679   Median :1.0005   Median : 4.620   Median :2.440  
#  Mean   : 1.8915   Mean   :1.0220   Mean   : 5.188   Mean   :2.492  
#  3rd Qu.: 2.4842   3rd Qu.:1.0993   3rd Qu.: 6.880   3rd Qu.:2.639  
#  Max.   : 4.1525   Max.   :1.4493   Max.   :17.126   Max.   :3.439  

转换为栅格

  
OK.pred<-rasterFromXYZ(as.data.frame(OK)[, c("x", "y", "OK.pred")])
OK.var<-rasterFromXYZ(as.data.frame(OK)[, c("x", "y", "OK.var")])

绘制预测 SOC 和 OK 误差

  
p1<-ggR(OK.pred, geom_raster = TRUE) +
scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("OK Predicted SOC")+
   theme(plot.title = element_text(hjust = 0.5))

p2<-ggR(OK.var, geom_raster = TRUE) +
scale_fill_gradientn("", colours = c("blue",  "green","yellow", "orange"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("OK Predition Variance")+
   theme(plot.title = element_text(hjust = 0.5))

grid.arrange(p1,p2, ncol = 2)  # Multiplot 

上图显示了土壤 SOC 的插值图，在每个预测网格上都具有相关的误差。OK 预测图显示了 SOC 浓度的全球模式和热点位置。kriging 方差在未采样位置中较高，因为方差取决于采样位置附近方差较低的采样位置的几何形状。该 kriging 方差也取决于 co 方差模型，但与数据值无关。

块克里金法

块克里金法与点克里金法相似。块克里金法，它估计网格 “块” 而不是单点的平均值。与单个点相比，这些块的预测误差通常较小。以块为中心的 kriging 估计通常与该点的 kriging 估计非常相似，但是，该预测是块平均值，它可以消除局部极端值，并且可以消除短程可变性 (在块内)，因此克里金方差低于点 OK。

像点 kriging 一样，我们可以使用 krige() 函数加上一个额外的参数:block，它以列表的形式给出块的维度。对于通常情况下的 2D block (表面积)，这是一个二维的列表(通常是，但不一定相同)。

  
OK.block <- krige(SOC.bc ~ 1, 
                 loc =  train, 
                 newdata = grid, 
                 model = m.f, 
                 block = c(50000, 50000)) # 50 km x 50 km
#  [using ordinary kriging]

逆变换

  
k1<-1/0.2523339                                   
OK.block$SOC.pred <-((OK.block$var1.pred *0.2523339+1)^k1)
OK.block$SOC.var <-((OK.block$var1.var *0.2523339+1)^k1)

转换为栅格

  
SOC.block.pred<-rasterFromXYZ(as.data.frame(OK.block)[, c("x", "y", "SOC.pred")])
SOC.block.var<-rasterFromXYZ(as.data.frame(OK.block)[, c("x", "y", "SOC.var")])

绘图

  
# Predicted values
p3<-ggR(SOC.block.pred, geom_raster = TRUE) +
scale_fill_gradientn("SOC", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("OK-Block Predicted SOC")+
   theme(plot.title = element_text(hjust = 0.5))

# Error
p4<-ggR(SOC.block.var, geom_raster = TRUE) +
scale_fill_gradientn("SOC", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("OK-Block Variance")+
   theme(plot.title = element_text(hjust = 0.5))

grid.arrange(p3,p4, ncol = 2)  # Multiplot 

泛克里金

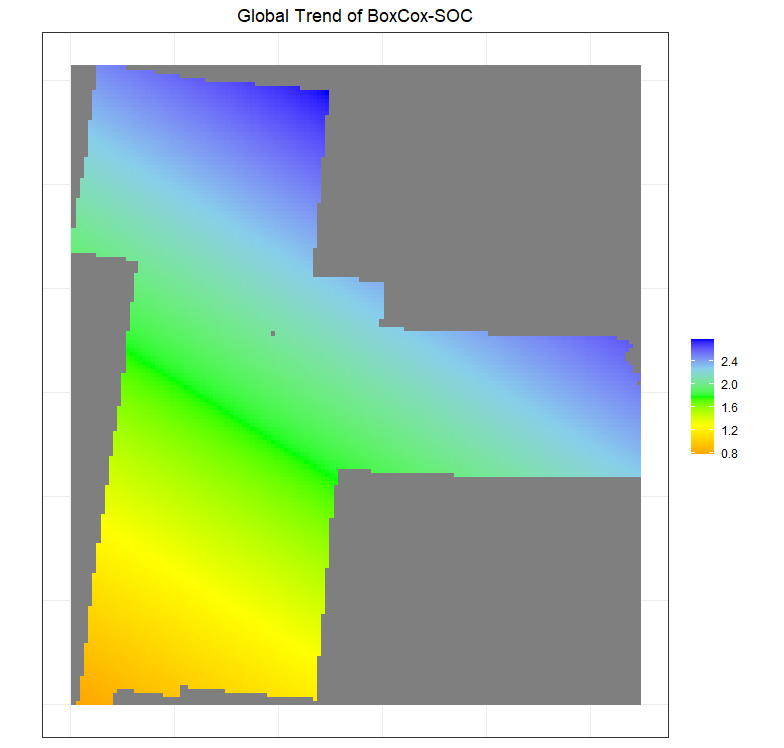
泛克里金法（UK）是普通克里金法在非平稳条件下的一种变体，在非平稳条件下，不同位置(趋势或漂移)的均值以确定的方式不同，而只有方差是恒定的。趋势可以拟合范围从局部(邻近地区)到全球(整个地区)，这种二阶平稳性(“弱平稳性”)通常是环境暴露的相关假设。在英国，通常首先将趋势计算为坐标的函数，然后将剩余的变化(残差)作为随机场添加到趋势中，以进行最终预测。

UK 模型将位置变量的值作为区域非平稳趋势和局部空间相关随机分量的和，即区域趋势的残差。

  
library(plyr)
library(dplyr)
library(gstat)
library(raster)
library(ggplot2)
library(car)
library(classInt)
library(RStoolbox)
library(spatstat)
library(dismo)
library(fields)
library(gridExtra)

# Define data folder
dataFolder<-"D:\\Env\\DATA_08\\"

train<-read.csv(paste0(dataFolder,"train_data.csv"), header= TRUE) 
test<-read.csv(paste0(dataFolder,"test_data.csv"), header= TRUE) 
state<-shapefile(paste0(dataFolder,"GP_STATE.shp"))
grid<-read.csv(paste0(dataFolder, "GP_prediction_grid_data.csv"), header= TRUE)

数据变换

  
powerTransform(train$SOC)
# Estimated transformation parameter 
# train$SOC 
# 0.2523339 

  
train$SOC.bc<-bcPower(train$SOC, 0.2523339)
# 必须为坐标定义x和y变量
coordinates(train) = ~x+y
coordinates(grid) = ~x+y

首先，我们将使用krige()函数计算并可视化一阶趋势面。

  
trend<-krige(SOC.bc~x+y, train, grid, model=NULL)
# [ordinary or weighted least squares prediction]

trend.r<-rasterFromXYZ(as.data.frame(trend)[, c("x", "y", "var1.pred")])
ggR(trend.r, geom_raster = TRUE) +
scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("Global Trend of BoxCox-SOC")+
   theme(plot.title = element_text(hjust = 0.5))

变异函数建模

在 UK 中，半方差基于残差，而不是原始数据，因为空间结构的随机部分仅适用于这些残差。残差的模型参数通常与原始的变异函数模型有很大不同 (通常: 较低的门槛，较短的范围)，因为全球趋势已经排除了一些变化和长期结构。在 gstat 中，如果我们提供适当的模型公式，我们可以直接计算残差变量; 您不必手动计算残差。

我们使用变异函数方法，并使用公式 SOC.bc〜x+y (与普通变异函数中的SOC.bc〜1相反) 指定空间依赖性。这与lm (线性回归) 模型规范中的含义相同: 使用 lst 顺序趋势预测 SOC 浓度; 然后在空间上对残差进行建模。

  
# Variogram
v<-variogram(SOC.bc~ x+y, data = train, cloud=F)
# Intial parameter set by eye esitmation
m<-vgm(1.5,"Exp",40000,0.5)
# least square fit
m.f<-fit.variogram(v, m)
m.f
#   model     psill    range
# 1   Nug 0.5186164     0.00
# 2   Exp 1.0744976 81954.85

绘制残差方差图和拟合模型

  
#### Plot varigram and fitted model:
plot(v, pl=F, 
     model=m.f,
     col="black", 
     cex=0.9, 
     lwd=0.5,
     lty=1,
     pch=19,
     main="Variogram of Residuals",
     xlab="Distance (m)",
     ylab="Semivariance")

克里金预测

gstat 包中的 krige() 函数用于简单，普通或通用的 kriging (有时称为外部漂移kriging)，局部邻域中的 kriging，块平均值 (矩形或不规则块) 的点 kriging 或kriging 以及所有 kriging 品种的条件 (高斯或指标) 模拟等效物，和反距离加权插值的函数。用于多变量预测。

  
UK<-krige(SOC.bc~x+y, 
              loc= train,        # Data frame
              newdata=grid,      # Prediction grid
              model = m.f)       # fitted varigram model
# [using universal kriging]
summary(UK)
# Object of class SpatialPointsDataFrame
# Coordinates:
#        min     max
# x -1245285  114715
# y  1003795 2533795
# Is projected: NA 
# proj4string : [NA]
# Number of points: 10674
# Data attributes:
#    var1.pred          var1.var     
#  Min.   :-0.1549   Min.   :0.7235  
#  1st Qu.: 1.2799   1st Qu.:0.9298  
#  Median : 1.8873   Median :1.0023  
#  Mean   : 1.8862   Mean   :1.0244  
#  3rd Qu.: 2.5169   3rd Qu.:1.1020  
#  Max.   : 4.1413   Max.   :1.4817  

逆变换

我们将使用使用过 Box-cos 变换的变换参数来逆变换。

  
k1<-1/0.2523339                                   
UK$UK.pred <-((UK$var1.pred *0.2523339+1)^k1)
UK$UK.var <-((UK$var1.var *0.2523339+1)^k1)
summary(UK)
# Object of class SpatialPointsDataFrame
# Coordinates:
#        min     max
# x -1245285  114715
# y  1003795 2533795
# Is projected: NA 
# proj4string : [NA]
# Number of points: 10674
# Data attributes:
#    var1.pred          var1.var         UK.pred            UK.var     
#  Min.   :-0.1549   Min.   :0.7235   Min.   : 0.8539   Min.   :1.944  
#  1st Qu.: 1.2799   1st Qu.:0.9298   1st Qu.: 3.0319   1st Qu.:2.305  
#  Median : 1.8873   Median :1.0023   Median : 4.6814   Median :2.444  
#  Mean   : 1.8862   Mean   :1.0244   Mean   : 5.2142   Mean   :2.497  
#  3rd Qu.: 2.5169   3rd Qu.:1.1020   3rd Qu.: 7.0191   3rd Qu.:2.644  
#  Max.   : 4.1413   Max.   :1.4817   Max.   :17.0323   Max.   :3.521  

转换为栅格

  
UK.pred<-rasterFromXYZ(as.data.frame(UK)[, c("x", "y", "UK.pred")])
UK.var<-rasterFromXYZ(as.data.frame(UK)[, c("x", "y", "UK.var")])

绘制预测 SOC 和 UK 误差

  
p1<-ggR(UK.pred, geom_raster = TRUE) +
scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("UK Predicted SOC")+
   theme(plot.title = element_text(hjust = 0.5))

p2<-ggR(UK.var, geom_raster = TRUE) +
scale_fill_gradientn("", colours = c("blue",  "green","yellow", "orange"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("UK Predition Variance")+
   theme(plot.title = element_text(hjust = 0.5))

grid.arrange(p1,p2, ncol = 2)  # Multiplot

上图显示了土壤 SOC 的插值图，在每个预测网格上都具有相关的误差。UK 预测图显示了 SOC 浓度的全球模式和热点位置。kriging 方差在未采样位置中较高，因为方差取决于采样位置附近方差较低的采样位置的几何形状。该 kriging 方差也取决于 co 方差模型，但与数据值无关。

协同克里金

协同克里金法 (CK) 是普通克里金法的扩展，其中使用了其他观察到的变量 (通常与感兴趣的变量相关的共同变量) 来提高感兴趣的变量的插值精度。与回归和泛克里金法不同，协同里格法不需要辅助信息在所有预测位置都可用。协变量可以在与目标 (共定位样本) 相同的点处、在其他点处或两者处测量。协克里金法最常见的应用是当协变量比目标变量更便宜的测量时。

首先，我们将探索SOC与其他环境协变量 (例如海拔，NDVI，TPI) 之间的关系，然后我们将选择一个与SOC关系最高的变量。此变量将用于SOC的cokriging。我们之前创建的土壤有机碳数据 (火车和测试数据集) 可从这里下载。

  
library(plyr)
library(dplyr)
library(gstat)
library(raster)
library(ggplot2)
library(car)
library(classInt)
library(RStoolbox)
library(spatstat)
library(dismo)
library(fields)
library(gridExtra)
library(Hmisc)

# Define data folder
dataFolder<-"D:\\Env\\DATA_08\\"

train<-read.csv(paste0(dataFolder,"train_data.csv"), header= TRUE) 
state<-shapefile(paste0(dataFolder,"GP_STATE.shp"))
grid<-read.csv(paste0(dataFolder, "GP_prediction_grid_data.csv"), header= TRUE) 

首先，我们将使用 SOC 和连续的环境数据创建一个 data.frame 。然后，我们将使用 Hmisc 包的 rcorr() 函数。我们将使用 Box-Cox 转换的 SOC 进行相关性分析。

幂变换

  
powerTransform(train$SOC)
# Estimated transformation parameter 
# train$SOC 
# 0.2523339

SOC.bc<-bcPower(train$SOC, 0.2523339)
train$SOC.bc<-bcPower(train$SOC, 0.2523339)

协区域化或 Corss-Varoigram 的变异函数模型

从相关性分析可以看出，只有 NDVI 与 SOC 的相关性最高 (r = 0.63，p 值 < 0.001)，因此将使用 NDVI 进行协同克里金。我们首先对目标变量 (SOC) 、协变量 (NDVI) 的空间结构及其与目标变量 (SOC) 的协方差进行建模。这被称为共同区域化。它是用于普通克里金法的单个区域主义变量理论的扩展。必须将直接方差图和交叉方差图一起建模，并带有一些限制，以确保可以解决所得的CK系统。使用以下公式计算交叉变异函数 (每对区域化变量):

定义坐标：

  
coordinates(train) = ~x+y
coordinates(grid) = ~x+y

目标变量直接方差图（SOC）

  
# Variogram
v.soc<-variogram(SOC.bc~ 1, data = train, cloud=F)
# Intial parameter set by eye esitmation
m.soc<-vgm(1.5,"Exp",400000,0.5)
# least square fit
m.f.soc<-fit.variogram(v.soc, m.soc)
p1<-plot(v.soc, pl=F, model=m.f.soc, main= "SOC")

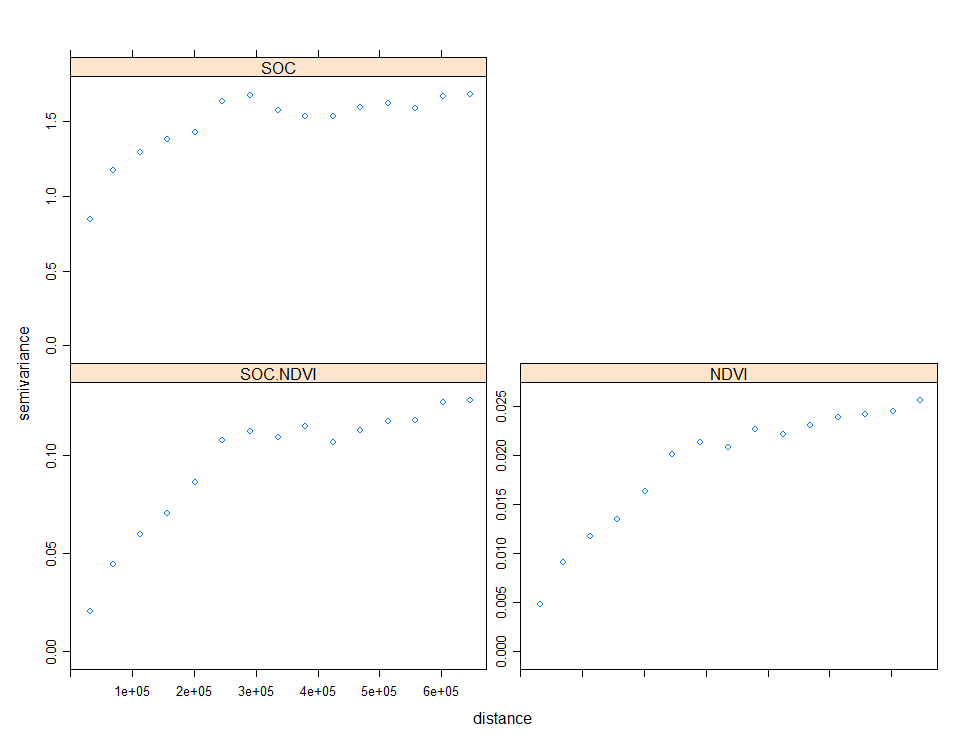
协变量变异函数建模的直接变异函数(NDVI)

  
# Variogram
v.ndvi<-variogram(NDVI~ 1, data = train, cloud=F)
# Intial parameter set by eye esitmation
m.ndvi<-vgm(1.5,"Exp",40000,0.5)
# least square fit
m.f.ndvi<-fit.variogram(v.ndvi, m.ndvi)
p2<-plot(v.ndvi, pl=F, model=m.f.ndvi, main="NDVI")

grid.arrange(p1, p2, ncol = 2)  # Multiplot 

交叉变异函数

为了对交叉变量进行建模，我们必须以相同的形状和范围同时将模型拟合到直接变量和交叉变量图，但可能具有不同的部分窗台和掘金。

对于R中的交叉变量建模，我们必须使用 gstat 方法依次构建 gstat 模型。首先，我们必须为目标 (SOC) 和协变量 (NDVI) 构建 gstat 结构。然后，添加我们将把变异函数模型拟合到 gstat 对象。

  
g <- gstat(NULL, id = "SOC", form = SOC.bc ~ 1, data=train)
g <- gstat(g, id = "NDVI", form = NDVI ~ 1, data=train)

显示两个直接变异函数和一个交叉变异函数：

  
v.cross <- variogram(g)
plot(v.cross, pl=F)

我们将在 gstat 对象中添加变异函数模型，并使用协区域化的线性模型对其进行拟合。通过用一个模型填充所有框架 (使用 fill.all = T 参数)，这些条件会自动满足。

  
#g <- gstat(g, id = "SOC", model = m.f.soc, fill.all=T)
g <- gstat(g, id = "SOC", model = m.f.soc, fill.all=T)
g
# data:
# SOC : formula = SOC.bc`~`1 ; data dim = 368 x 22
# NDVI : formula = NDVI`~`1 ; data dim = 368 x 22
# variograms:
#             model     psill    range
# SOC[1]        Nug 0.5165078     0.00
# SOC[2]        Exp 1.0817190 82362.04
# NDVI[1]       Nug 0.5165078     0.00
# NDVI[2]       Exp 1.0817190 82362.04
# SOC.NDVI[1]   Nug 0.5165078     0.00
# SOC.NDVI[2]   Exp 1.0817190 82362.04

现在，我们将所有三个变异函数放在一起，以确保它们导致正定共克里金系统。为此，我们使用 fit.lmc 方法 (“协同区域化的拟合线性模型”)。这将采用初始估计值，拟合所有变异函数，然后将每个部分窗台 (通过最小二乘法) 调整为最接近的值，这将导致正定矩阵。

  
g <- fit.lmc(v.cross, g)
g
# data:
# SOC : formula = SOC.bc`~`1 ; data dim = 368 x 22
# NDVI : formula = NDVI`~`1 ; data dim = 368 x 22
# variograms:
#             model        psill    range
# SOC[1]        Nug  0.516509101     0.00
# SOC[2]        Exp  1.081719638 82362.04
# NDVI[1]       Nug  0.001006654     0.00
# NDVI[2]       Exp  0.018584071 82362.04
# SOC.NDVI[1]   Nug -0.022802328     0.00
# SOC.NDVI[2]   Exp  0.125599263 82362.04

  
plot(variogram(g), model=g$model)

网格位置的协同克里金法预测

用于 OK 的包装器方法 krige() 只能用于单变量 kriging; 这里我们必须使用 predict() 函数。这将 gstat 对象作为第一个参数，并将预测点数据框作为第二个参数。

  
CK <- predict(g, grid)
# Linear Model of Coregionalization found. Good.
# [using ordinary cokriging]

  
summary(CK)
# Object of class SpatialPointsDataFrame
# Coordinates:
#        min     max
# x -1245285  114715
# y  1003795 2533795
# Is projected: NA 
# proj4string : [NA]
# Number of points: 10674
# Data attributes:
#     SOC.pred         SOC.var         NDVI.pred         NDVI.var         cov.SOC.NDVI     
#  Min.   :-0.146   Min.   :0.5951   Min.   :0.1565   Min.   :0.001187   Min.   :-0.02614  
#  1st Qu.: 1.170   1st Qu.:0.8408   1st Qu.:0.3090   1st Qu.:0.005756   1st Qu.: 0.00624  
#  Median : 1.805   Median :0.9288   Median :0.4035   Median :0.007375   Median : 0.01757  
#  Mean   : 1.854   Mean   :0.9461   Mean   :0.4185   Mean   :0.007672   Mean   : 0.01955  
#  3rd Qu.: 2.525   3rd Qu.:1.0345   3rd Qu.:0.5125   3rd Qu.:0.009305   3rd Qu.: 0.03097  
#  Max.   : 4.272   Max.   :1.4296   Max.   :0.7758   Max.   :0.016465   Max.   : 0.08082  

逆变换

我们将使用使用 Box-cos 转换的转换参数进行逆转换。

  
k1<-1/0.2523339                                   
CK$CK.pred <-((CK$SOC.pred *0.2523339+1)^k1)
CK$CK.var <-((CK$SOC.var *0.2523339+1)^k1)
summary(CK)
# Object of class SpatialPointsDataFrame
# Coordinates:
#        min     max
# x -1245285  114715
# y  1003795 2533795
# Is projected: NA 
# proj4string : [NA]
# Number of points: 10674
# Data attributes:
#     SOC.pred         SOC.var         NDVI.pred         NDVI.var         cov.SOC.NDVI     
#  Min.   :-0.146   Min.   :0.5951   Min.   :0.1565   Min.   :0.001187   Min.   :-0.02614  
#  1st Qu.: 1.170   1st Qu.:0.8408   1st Qu.:0.3090   1st Qu.:0.005756   1st Qu.: 0.00624  
#  Median : 1.805   Median :0.9288   Median :0.4035   Median :0.007375   Median : 0.01757  
#  Mean   : 1.854   Mean   :0.9461   Mean   :0.4185   Mean   :0.007672   Mean   : 0.01955  
#  3rd Qu.: 2.525   3rd Qu.:1.0345   3rd Qu.:0.5125   3rd Qu.:0.009305   3rd Qu.: 0.03097  
#  Max.   : 4.272   Max.   :1.4296   Max.   :0.7758   Max.   :0.016465   Max.   : 0.08082  
#     CK.pred            CK.var     
#  Min.   : 0.8617   Min.   :1.741  
#  1st Qu.: 2.7875   1st Qu.:2.144  
#  Median : 4.4252   Median :2.303  
#  Mean   : 5.1919   Mean   :2.349  
#  3rd Qu.: 7.0556   3rd Qu.:2.507  
#  Max.   :18.1452   Max.   :3.390 

转换为栅格

  
CK.pred<-rasterFromXYZ(as.data.frame(CK)[, c("x", "y", "CK.pred")])
CK.var<-rasterFromXYZ(as.data.frame(CK)[, c("x", "y", "CK.var")])

绘制预测 SOC 和 CK 误差

  
p3<-ggR(CK.pred, geom_raster = TRUE) +
scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("CK Predicted SOC")+
   theme(plot.title = element_text(hjust = 0.5))

p4<-ggR(CK.var, geom_raster = TRUE) +
scale_fill_gradientn("", colours = c("blue",  "green","yellow", "orange"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("CK Predition Variance")+
   theme(plot.title = element_text(hjust = 0.5))

grid.arrange(p3,p4, ncol = 2)  # Multiplot

上图显示了土壤 SOC 的插值图，在每个预测网格上都具有相关的误差。CK 预测图显示了 SOC 浓度的全球模式和热点位置。kriging 方差在未采样位置中较高，因为方差取决于采样位置附近方差较低的采样位置的几何形状。

回归克里金

在这个练习中，我们将使用以下回归模型对 SOC 进行回归克里金:

广义线性模型
随机森林
元集成机器学习

我们将使用插入 caret 包进行回归，使用 gstat 包进行地理统计建模。

  
library(plyr)
library(dplyr)
library(gstat)
library(raster)
library(ggplot2)
library(car)
library(classInt)
library(RStoolbox)
library(caret)
library(caretEnsemble)
library(doParallel)
library(gridExtra)

# Define data folder
dataFolder<-"D:\\Env\\DATA_08\\"

train<-read.csv(paste0(dataFolder,"train_data.csv"), header= TRUE) 
state<-shapefile(paste0(dataFolder,"GP_STATE.shp"))
grid<-read.csv(paste0(dataFolder, "GP_prediction_grid_data.csv"), header= TRUE)

首先，我们将创建一个具有 SOC 和连续环境数据的 data.frame。

幂变换

  
powerTransform(train$SOC)
## Estimated transformation parameter 
## train$SOC 
## 0.2523339
train$SOC.bc<-bcPower(train$SOC, 0.2523339)

创建 dataframes

  
# train data
train.xy<-train[,c(1,24,8:9)]
train.df<-train[,c(1,24,11:21)]
# grid data
grid.xy<-grid[,c(1,2:3)]
grid.df<-grid[,c(4:14)]
#  define response & predictors
RESPONSE<-train.df$SOC.bc
train.x<-train.df[3:13]

坐标系：

  
coordinates(train.xy) = ~x+y
coordinates(grid.xy) = ~x+y

开始foreach并行化以进行模型拟合

  
mc <- makeCluster(detectCores())
registerDoParallel(mc)

设置控制参数

  
myControl <- trainControl(method="repeatedcv", 
                          number=10, 
                          repeats=5,
                          allowParallel = TRUE)

广义线性模型

广义线性模型 (GLM) 是普通线性回归的灵活概括，它允许响应变量具有除正态分布之外的误差分布模型。

首先将GLM模型与一个综合的环境协变量进行拟合，然后，我们将计算和建模 GLM 模型的残差的变异函数，然后将简单的克里金法 (SK) 应用于残差估计残差的空间预测 (区域趋势)。最后，GLM回归预测结果，将添加SK克里金残差来估计插值土壤有机碳。

拟合广义线性模型 (GLM)

  
set.seed(1856)
GLM<-train(train.x,
           RESPONSE,
           method = "glm",
           trControl=myControl,
           preProc=c('center', 'scale'))
print(GLM)
# Generalized Linear Model 

# 368 samples
#  11 predictor

# Pre-processing: centered (11), scaled (11) 
# Resampling: Cross-Validated (10 fold, repeated 5 times) 
# Summary of sample sizes: 332, 331, 331, 331, 332, 331, ... 
# Resampling results:

#   RMSE       Rsquared   MAE      
#   0.9423772  0.4742412  0.7310591

GLM 残差的变异函数建模

首先，我们必须提取 GLM 模型的残差，我们将使用 resid() 函数来获取 GLM 模型的残差。

  
# 提取残差
train.xy$residuals.glm<-resid(GLM)
# Variogram
v.glm<-variogram(residuals.glm~ 1, data = train.xy,cutoff=300000, width=300000/15)
# Intial parameter set by eye esitmation
m.glm<-vgm(0.15,"Exp",40000,0.05)
# 最小二乘拟合
m.f.glm<-fit.variogram(v.glm, m.glm)
m.f.glm
#   model     psill    range
# 1   Nug 0.1085947     0.00
# 2   Exp 0.7943117 18818.22

  
#### Plot varigram and fitted model:
plot(v.glm, pl=F, 
     model=m.f.glm,
     col="black", 
     cex=0.9, 
     lwd=0.5,
     lty=1,
     pch=19,
     main="Variogram and Fitted Model\n Residuals of GLM model",
     xlab="Distance (m)",
     ylab="Semivariance")

网格位置的GLM预测

  
grid.xy$GLM <- predict(GLM, grid.df)

网格位置GLM残差的简单克里金法预测

  
SK.GLM<-krige(residuals.glm~ 1, 
              loc=train.xy,        # Data frame
              newdata=grid.xy,     # Prediction location
              model = m.f.glm,     # fitted varigram model
              beta = 0)            # residuals from a trend; expected value is 0 
# [using simple kriging]

克里金法预测 (SK + 回归预测)

  
grid.xy$SK.GLM<-SK.GLM$var1.pred
# 添加 RF 预测 + SK 预测残差
grid.xy$RK.GLM.bc<-(grid.xy$GLM+grid.xy$SK.GLM)

逆变换

对于逆变换，我们使用变换参数：

  
k1<-1/0.2523339                                   
grid.xy$RK.GLM <-((grid.xy$RK.GLM.bc *0.2523339+1)^k1)
summary(grid.xy)
# Object of class SpatialPointsDataFrame
# Coordinates:
#        min     max
# x -1245285  114715
# y  1003795 2533795
# Is projected: NA 
# proj4string : [NA]
# Number of points: 10674
# Data attributes:
#        ID             GLM              SK.GLM            RK.GLM.bc          RK.GLM       
#  Min.   :    1   Min.   :-0.9197   Min.   :-2.663611   Min.   :-1.084   Min.   : 0.2819  
#  1st Qu.: 2772   1st Qu.: 1.1693   1st Qu.:-0.104815   1st Qu.: 1.130   1st Qu.: 2.7028  
#  Median : 5510   Median : 1.7494   Median : 0.008580   Median : 1.742   Median : 4.2374  
#  Mean   : 5499   Mean   : 1.8277   Mean   : 0.001208   Mean   : 1.829   Mean   : 5.3003  
#  3rd Qu.: 8237   3rd Qu.: 2.4885   3rd Qu.: 0.130163   3rd Qu.: 2.553   3rd Qu.: 7.1747  
#  Max.   :10999   Max.   : 4.2655   Max.   : 1.663093   Max.   : 4.995   Max.   :25.3268  

转换为栅格

  
GLM<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "GLM")])
SK.GLM<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "SK.GLM")])
RK.GLM.bc<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "RK.GLM.bc")])
RK.GLM.SOC<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "RK.GLM")])

绘制预测 SOC

  
glm1<-ggR(GLM, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("GLM Predicted (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

glm2<-ggR(SK.GLM, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("SK GLM Residuals (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

glm3<-ggR(RK.GLM.bc, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("RK-GLM Predicted (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

glm4<-ggR(RK.GLM.SOC, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("RK-GLM Predicted (mg/g)")+
   theme(plot.title = element_text(hjust = 0.5))

grid.arrange(glm1,glm2,glm3,glm4, ncol = 4)  # Multiplot 

随机森林

基于决策树的多次迭代组合的随机森林已经成为一种主要的数据分析工具，与单次迭代分类和回归树分析相比表现良好 [Heidema等，2006]。每棵树都是通过引导原始数据集制成的，该原始数据集允许使用剩余的测试集 (所谓的袋外 (Out-Of-Bag，OOB) 样本) 进行稳健的误差估计。从引导样本中预测排除的 OOB 样本，并通过组合所有树的 OOB 预测。RF 算法可以优于线性回归，与线性回归不同，RF 没有考虑目标变量的概率密度函数形式的要求 [Hengl等，2015; Kuhn和Johnson，2013]。RF 的一个主要缺点是难以解释响应和预测变量之间的关系。但是，RF 允许通过置换 OOB 变量之前和之后预测精度的平均下降来估计变量的重要性。然后在所有树上对两者之间的差异进行平均，并通过差异的标准偏差进行归一化 (Ahmed等，2017)。

首先，用一个综合的环境协变量拟合 RF 模型，然后，我们将计算和建模 RF 模型残差的变异函数，然后将简单的克里金法 (SK) 应用于残差，以估计空间预测残差 (区域趋势)。最后，RF 回归预测结果，将添加 SK 克里金残差来估计插值土壤有机碳。

拟合随机森林模型 (RF)

  
set.seed(1856)
mtry <- sqrt(ncol(train.x))  # 每次拆分时随机抽样作为候选变量的数量。
tunegrid.rf <- expand.grid(.mtry=mtry)
RF<-train(train.x,
           RESPONSE,
           method = "rf",
           trControl=myControl,
           tuneGrid=tunegrid.rf,
           ntree= 100,
           preProc=c('center', 'scale'))
print(RF)
# Random Forest 

# 368 samples
#  11 predictor

# Pre-processing: centered (11), scaled (11) 
# Resampling: Cross-Validated (10 fold, repeated 5 times) 
# Summary of sample sizes: 332, 331, 331, 331, 332, 331, ... 
# Resampling results:

#   RMSE       Rsquared   MAE      
#   0.9345237  0.4780398  0.7210278

# Tuning parameter 'mtry' was held constant at a value of 3.316625

RF 残差的变异函数建模

首先，我们必须提取 RF 模型的残差，我们将使用 resid() 函数来获取 RF 模型的残差。

  
# Extract residials
train.xy$residuals.rf<-resid(RF)
# Variogram
v.rf<-variogram(residuals.rf~ 1, data = train.xy)
# Intial parameter set by eye esitmation
m.rf<-vgm(0.15,"Exp",40000,0.05)
# least square fit
m.f.rf<-fit.variogram(v.rf, m.rf)
m.f.rf
#   model     psill    range
# 1   Nug 0.0000000     0.00
# 2   Exp 0.1934731 15626.27

  
#### Plot varigram and fitted model:
plot(v.rf, pl=F, 
     model=m.f.rf,
     col="black", 
     cex=0.9, 
     lwd=0.5,
     lty=1,
     pch=19,
     main="Variogram and Fitted Model\n Residuals of RF model",
     xlab="Distance (m)",
     ylab="Semivariance")

网格位置的预测

  
grid.xy$RF <- predict(RF, grid.df)

网格位置处 RF 残差的简单 Kriging 预测

  
SK.RF<-krige(residuals.rf~ 1, 
              loc=train.xy,        # Data frame
              newdata=grid.xy,     # Prediction location
              model = m.f.rf,      # fitted varigram model
              beta = 0)            # residuals from a trend; expected value is 0 
# [using simple kriging]

克里金法预测 (SK + 回归)

  
grid.xy$SK.RF<-SK.RF$var1.pred
# Add RF predicted + SK preedicted residuals
grid.xy$RK.RF.bc<-(grid.xy$RF+grid.xy$SK.RF)

逆变换

对于逆变换，我们使用变换参数：

  
k1<-1/0.2523339                                   
grid.xy$RK.RF <-((grid.xy$RK.RF.bc *0.2523339+1)^k1)
summary(grid.xy)
# Object of class SpatialPointsDataFrame
# Coordinates:
#        min     max
# x -1245285  114715
# y  1003795 2533795
# Is projected: NA 
# proj4string : [NA]
# Number of points: 10674
# Data attributes:
#        ID             GLM              SK.GLM            RK.GLM.bc          RK.GLM       
#  Min.   :    1   Min.   :-0.9197   Min.   :-2.663611   Min.   :-1.084   Min.   : 0.2819  
#  1st Qu.: 2772   1st Qu.: 1.1693   1st Qu.:-0.104815   1st Qu.: 1.130   1st Qu.: 2.7028  
#  Median : 5510   Median : 1.7494   Median : 0.008580   Median : 1.742   Median : 4.2374  
#  Mean   : 5499   Mean   : 1.8277   Mean   : 0.001208   Mean   : 1.829   Mean   : 5.3003  
#  3rd Qu.: 8237   3rd Qu.: 2.4885   3rd Qu.: 0.130163   3rd Qu.: 2.553   3rd Qu.: 7.1747  
#  Max.   :10999   Max.   : 4.2655   Max.   : 1.663093   Max.   : 4.995   Max.   :25.3268  
#        RF              SK.RF               RK.RF.bc           RK.RF        
#  Min.   :-0.2965   Min.   :-1.0396339   Min.   :-0.8629   Min.   : 0.3779  
#  1st Qu.: 1.1496   1st Qu.:-0.0487090   1st Qu.: 1.1342   1st Qu.: 2.7114  
#  Median : 1.8344   Median :-0.0008605   Median : 1.8129   Median : 4.4496  
#  Mean   : 1.8425   Mean   :-0.0063920   Mean   : 1.8361   Mean   : 5.2190  
#  3rd Qu.: 2.5434   3rd Qu.: 0.0401477   3rd Qu.: 2.5500   3rd Qu.: 7.1623  
#  Max.   : 4.6236   Max.   : 1.0526308   Max.   : 5.2743   Max.   :28.6076 

转换为栅格

  
RF<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "RF")])
SK.RF<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "SK.RF")])
RK.RF.bc<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "RK.RF.bc")])
RK.RF.SOC<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "RK.RF")])

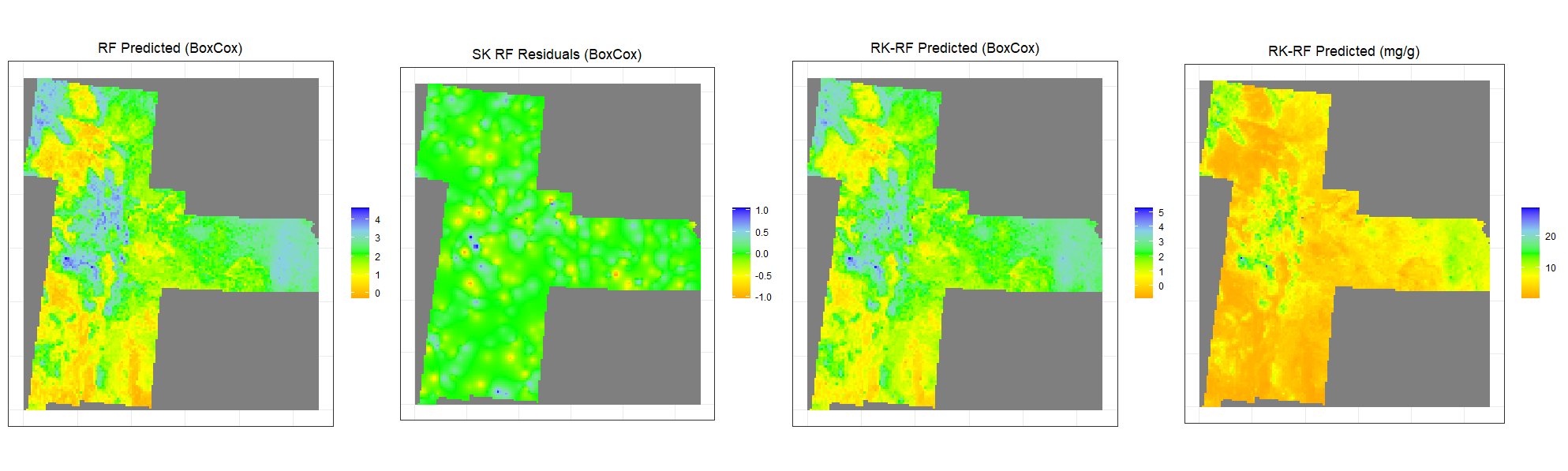
绘制预测 SOC

  
rf1<-ggR(RF, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("RF Predicted (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

rf2<-ggR(SK.RF, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("SK RF Residuals (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

rf3<-ggR(RK.RF.bc, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("RK-RF Predicted (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

rf4<-ggR(RK.RF.SOC, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("RK-RF Predicted (mg/g)")+
   theme(plot.title = element_text(hjust = 0.5))

grid.arrange(rf1,rf2,rf3,rf4, ncol = 4)  # Multiplot

元集成机器学习

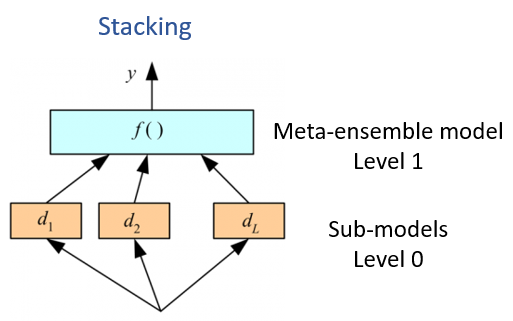
集成机器学习方法使用多种学习算法来获得比从任何组成学习算法获得的更好的预测性能。许多流行的现代机器学习算法都是集合。例如，随机森林和梯度提升机都是集合学习器。但是，堆叠泛化或堆叠或超级学习 (Wolpert，1992) 引入了元学习器的概念，该概念将多个强大的，不同的机器学习模型集合或组合在一起以获得更好的预测。在这种建模方法中，首先训练每个基本级别模型，然后在基本级别模型的输出上训练元模型。基本级别模型通常由不同的学习算法组成，因此堆叠集合通常是异构的。

我们将 GLM 和 RF 回归模型(子模型)叠加，建立随机森林 (RF) 回归模型来预测 SOC。

创建模型列表

  
algorithmList <- c("glm","rf")

拟合所有模型

我们将使用 caretEnsemble 包的 caretList() 功能来拟合所有模型。

  
set.seed(1856)
models<-caretList(train.x, RESPONSE,
                  methodList=algorithmList,
                  trControl=myControl,
                  preProc=c('center', 'scale'))

子模型的性能

  
results.all <- resamples(models)
cv.models<-as.data.frame(results.all[2])
summary(results.all)
# Call:
# summary.resamples(object = results.all)

# Models: glm, rf 
# Number of resamples: 50 

# MAE 
#          Min.   1st Qu.    Median      Mean   3rd Qu.     Max. NA's
# glm 0.5299362 0.6759200 0.7317607 0.7323044 0.7936931 1.049905    0
# rf  0.5559114 0.6511738 0.7138410 0.7195130 0.7839459 1.010871    0

# RMSE 
#          Min.   1st Qu.    Median      Mean  3rd Qu.     Max. NA's
# glm 0.6654767 0.8742916 0.9524959 0.9435913 1.034049 1.308432    0
# rf  0.6854099 0.8645415 0.9399393 0.9306508 1.010455 1.261128    0

# Rsquared 
#          Min.   1st Qu.    Median      Mean   3rd Qu.      Max. NA's
# glm 0.1626709 0.4161093 0.4726874 0.4767778 0.5456160 0.6850497    0
# rf  0.2138578 0.4080458 0.4848379 0.4868120 0.5505441 0.7026729    0

绘制 K 折交叉验证结果 (MAE，RMSE，R2)

  
dotplot(results.all, 
        scales =list(x = list(relation = "free")),
        panelRange =T,  conf.level = 0.9, 
        between = list(x = 2), layout=c(3,1))

通过叠加来组合几个预测模型

对于随机森林回归模型，我们将使用带有 method 和 rf 参数的 caretStack() 函数:

  
stackControl <- trainControl(method="repeatedcv", 
                             number=10, 
                             repeats=5, 
                             savePredictions=TRUE)
set.seed(1856)
stack.rf <- caretStack(models, 
                       method="rf",
                       trControl=stackControl)
# note: only 1 unique complexity parameters in default grid. Truncating the grid to 1 .

集合结果

  
stack.rf.cv<-stack.rf$ens_model$resample
stack.rf.results<-print(stack.rf)
# A rf ensemble of 2 base models: glm, rf

# Ensemble results:
# Random Forest 

# 1840 samples
#    2 predictor

# No pre-processing
# Resampling: Cross-Validated (10 fold, repeated 5 times) 
# Summary of sample sizes: 1656, 1656, 1656, 1656, 1656, 1656, ... 
# Resampling results:

#   RMSE       Rsquared   MAE      
#   0.8861827  0.5296594  0.6690021

# Tuning parameter 'mtry' was held constant at a value of 2

残差的变异函数建模

现在，我们将计算 RF 模型的残差，因为 resid() 函数在这里不起作用。

  
train.xy$REG.SOC.bc<-predict(stack.rf,train.x)
train.xy$residuals.stack<-(train.xy$SOC.bc-train.xy$REG.SOC.bc)

# Variogram
v.stack<-variogram(residuals.stack~ 1, data = train.xy)
# Intial parameter set by eye esitmation
m.stack<-vgm(0.15,"Exp",40000,0.05)
# least square fit
m.f.stack<-fit.variogram(v.stack, m.stack)
m.f.stack
#   model      psill    range
# 1   Nug 0.74019315      0.0
# 2   Exp 0.02392722 196106.8

  
#### Plot varigram and fitted model:
plot(v.stack, pl=F, 
     model=m.f.stack,
     col="black", 
     cex=0.9, 
     lwd=0.5,
     lty=1,
     pch=19,
     main="Variogram and Fitted Model\n Residuals of meta-Ensemble model",
     xlab="Distance (m)",
     ylab="Semivariance")

网格位置的预测

  
grid.xy$stack <- predict(stack.rf, grid.df)

网格位置处 RF 残差的简单 Kriging 预测

  
SK.stack<-krige(residuals.stack~ 1, 
              loc=train.xy,        # Data frame
              newdata=grid.xy,     # Prediction location
              model = m.f.stack,    # fitted varigram model
              beta = 0)            # residuals from a trend; expected value is 0  
# [using simple kriging]

克里金法预测 (SK + 回归)

  
grid.xy$SK.stack<-SK.stack$var1.pred
# Add RF predicted + SK preedicted residuals
grid.xy$RK.stack.bc<-(grid.xy$stack+grid.xy$SK.stack)

逆变换

  
k1<-1/0.2523339                                   
grid.xy$RK.stack <-((grid.xy$RK.stack.bc *0.2523339+1)^k1)
summary(grid.xy)
# Object of class SpatialPointsDataFrame
# Coordinates:
#        min     max
# x -1245285  114715
# y  1003795 2533795
# Is projected: NA 
# proj4string : [NA]
# Number of points: 10674
# Data attributes:
#        ID             GLM              SK.GLM            RK.GLM.bc          RK.GLM       
#  Min.   :    1   Min.   :-0.9197   Min.   :-2.663611   Min.   :-1.084   Min.   : 0.2819  
#  1st Qu.: 2772   1st Qu.: 1.1693   1st Qu.:-0.104815   1st Qu.: 1.130   1st Qu.: 2.7028  
#  Median : 5510   Median : 1.7494   Median : 0.008580   Median : 1.742   Median : 4.2374  
#  Mean   : 5499   Mean   : 1.8277   Mean   : 0.001208   Mean   : 1.829   Mean   : 5.3003  
#  3rd Qu.: 8237   3rd Qu.: 2.4885   3rd Qu.: 0.130163   3rd Qu.: 2.553   3rd Qu.: 7.1747  
#  Max.   :10999   Max.   : 4.2655   Max.   : 1.663093   Max.   : 4.995   Max.   :25.3268  
#        RF              SK.RF               RK.RF.bc           RK.RF        
#  Min.   :-0.2965   Min.   :-1.0396339   Min.   :-0.8629   Min.   : 0.3779  
#  1st Qu.: 1.1496   1st Qu.:-0.0487090   1st Qu.: 1.1342   1st Qu.: 2.7114  
#  Median : 1.8344   Median :-0.0008605   Median : 1.8129   Median : 4.4496  
#  Mean   : 1.8425   Mean   :-0.0063920   Mean   : 1.8361   Mean   : 5.2190  
#  3rd Qu.: 2.5434   3rd Qu.: 0.0401477   3rd Qu.: 2.5500   3rd Qu.: 7.1623  
#  Max.   : 4.6236   Max.   : 1.0526308   Max.   : 5.2743   Max.   :28.6076  
#      stack           SK.stack         RK.stack.bc        RK.stack      
#  Min.   :-1.218   Min.   :-0.21691   Min.   :-1.257   Min.   : 0.2205  
#  1st Qu.: 1.126   1st Qu.:-0.05766   1st Qu.: 1.117   1st Qu.: 2.6744  
#  Median : 1.826   Median :-0.02026   Median : 1.804   Median : 4.4215  
#  Mean   : 1.840   Mean   :-0.01805   Mean   : 1.822   Mean   : 5.3440  
#  3rd Qu.: 2.578   3rd Qu.: 0.01338   3rd Qu.: 2.552   3rd Qu.: 7.1725  
#  Max.   : 5.223   Max.   : 0.17909   Max.   : 5.202   Max.   :27.7264  

转换为栅格

  
stack<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "stack")])
SK.stack<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "SK.stack")])
RK.stack.bc<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "RK.stack.bc")])
RK.stack.SOC<-rasterFromXYZ(as.data.frame(grid.xy)[, c("x", "y", "RK.stack")])

绘制预测 SOC

  
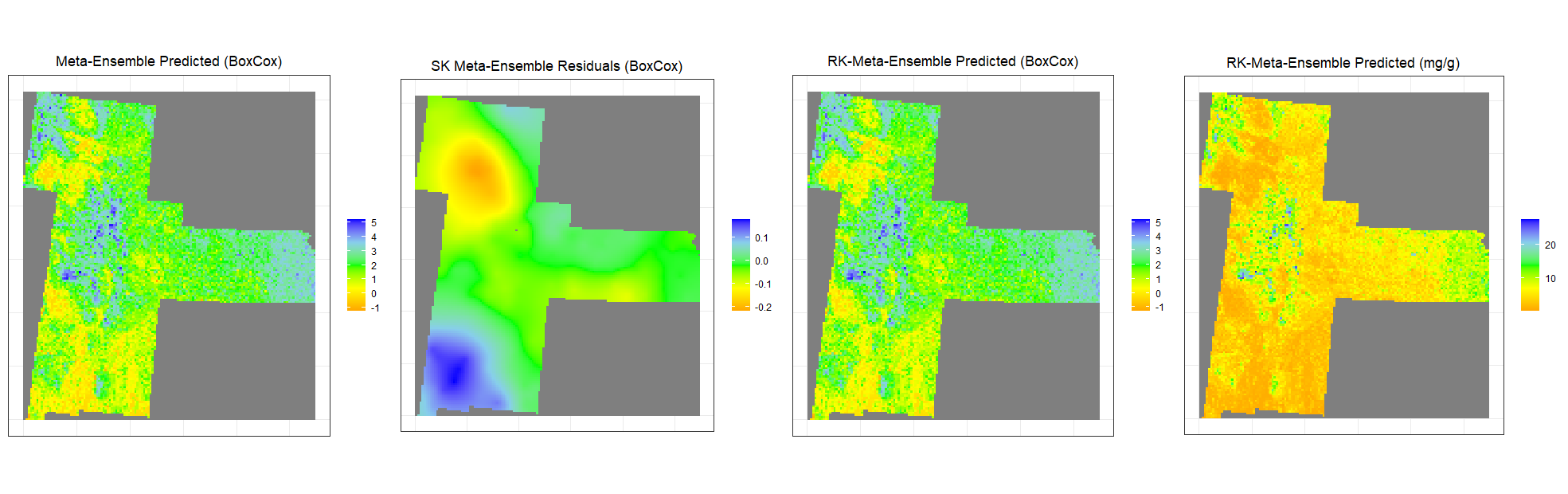
s1<-ggR(stack, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("Meta-Ensemble Predicted (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

s2<-ggR(SK.stack, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("SK Meta-Ensemble Residuals (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

s3<-ggR(RK.stack.bc, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("RK-Meta-Ensemble Predicted (BoxCox)")+
   theme(plot.title = element_text(hjust = 0.5))

s4<-ggR(RK.stack.SOC, geom_raster = TRUE) +
  scale_fill_gradientn("", colours = c("orange", "yellow", "green",  "sky blue","blue"))+
  theme_bw()+
    theme(axis.title.x=element_blank(),
        axis.text.x=element_blank(),
        axis.ticks.x=element_blank(),
        axis.title.y=element_blank(),
        axis.text.y=element_blank(),
        axis.ticks.y=element_blank())+
   ggtitle("RK-Meta-Ensemble Predicted (mg/g)")+
   theme(plot.title = element_text(hjust = 0.5))

grid.arrange(s1,s2,s3,s4, ncol = 4)  # Multiplot 

指示克里金

指示 kriging (IK) 是一种非参数地统计学方法，它对预先定义的阈值进行指标变换 (0,1) 后的变量进行工作，并映射超过预先定义的阈值的概率。这对于概率决策是直接有用的。它还可以用于估计整个累积概率分布 (CDF)，并且CDF的平均值 (E型估计) 可以用作对分布的上尾和下尾进行建模之后的污染物浓度的估计 (Goovaerts，2009)。基于CDF的IK适用于数据强烈偏斜时，传统的数据转换限制了由于极端值而获得稳健的统计数据和估计量。

在 R 中使用 gstat 包，我们可以实现指示克里金(IK)进行概率映射。但是目前还没有可用的 R 包来通过 IK 的 CDF 的 E-type-estimate。您可以使用最流行的地质统计软件 Gslib 和 sems 来完成。AUTO-IK(Goovaerts, 2009)，是一种自动的Gslib例程，用于连续数据二进制编码的阈值选择，指标半变差函数的计算和建模，非监控位置(规则或不规则网格)概率分布的建模，以及这些分布的均值和方差的估计。

本工作将使用英国地质调查局提供的孟加拉国地下水砷浓度数据。数据库包含孟加拉国64个区中 61 个区的 3534 个钻孔调查的水化学数据。)．约 27.7% 和 2.5% 的样品井 As 浓度分别低于氢化物发生-原子荧光光谱法 0.5 u/L 和氢化物发生-ICP-AES 法 6.0 ug/L的仪器检测限。As凝结低于检出限的样品，我们指定的值为设备检出限的一半(0.25或3.0 ug/l)。

土壤有机碳数据(训练和试验数据集)可以在这里找到。

我们将使用两个阈值 -10 ppb (WHO标准) 和 50 ppb (孟加拉国标准) 来创建超出这些阈值的概率图，我们将按照以下步骤进行操作:

将数值变量转换为指示器变量
计算并建立指标变异函数模型
通过指示克里金预测超过阈值的概率

  
library(plyr)
library(dplyr)
library(gstat)
library(raster)
library(rasterVis)
library(ggplot2)
library(car)
library(classInt)
library(RStoolbox)
library(gridExtra)

# Define data folder
dataFolder<-"D:\\Env\\DATA_08\\"

df<-read.csv(paste0(dataFolder,"bgs_geochemical.csv"), header= TRUE) 
grid<-read.csv(paste0(dataFolder,"bd_grid.csv"), header= TRUE) 
bd<-shapefile(paste0(dataFolder,"BD_Banladesh_BUTM.shp"))

探索性数据分析

  
summary(df$As)
#    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#    0.25    0.25    3.90   55.17   49.98 1660.00 

  
par(mfrow=c(1,2))
hist(df$As, breaks=20, xlab = "As (ppb)", main="Histogram of As")
box()
qqnorm(df$As, pch = 1,main= "QQ-plot of As") 
qqline(df$As, col = "steelblue", lwd = 2) 

par(mfrow=c(1,1))

创建 SPDF

所有采样位置都在地理坐标系统中，因此我们需要在投影坐标系中转换数据 (Albers等面积Conic NAD1983)

  
##  define coordinates
xy <- df[,c(4,5)]
# Convert to spatial point
SPDF <- SpatialPointsDataFrame(coords = xy, data=df) 
# Define projection
proj4string(SPDF) = CRS("+proj=longlat +ellps=WGS84")  # WGS 84
# Change projection 
BUTM<-proj4string(bd)              # extract projection information
SPDF.PROJ<- spTransform(SPDF,        # Input SPDF
                          BUTM)       # projection 

  
# convert to a data-frame
point.df<-as.data.frame(SPDF.PROJ)
# Rename (last two column)
colnames(point.df)[35] <- "x"
colnames(point.df)[36] <- "y"
mf<-point.df[,c(35:36,7,15,23)]
head(mf)
#          x       y WELL_TYPE  As    Fe
# 1 509574.3 2474006       DTW 0.5 0.103
# 2 439962.9 2647931       STW 0.5 0.087
# 3 662328.1 2718502       STW 0.5  1.37
# 4 619708.4 2631583       STW 0.5 0.128
# 5 454332.2 2522667       DTW 0.5 0.019
# 6 438852.0 2576967       STW 0.5 0.042

指标变换

现在，我们使用以下公式计算阈值400 ppm Pb的指标变量。如果连续变量的值低于定义的阈值，则连续变量的指标为1，否则为0。

  
ik.10<-mf$As > 10    # threshold 10 ppb
ik.50<-mf$As > 50    # threshold 50 ppb

现在，我们用这个指标创建一个df。

  
ik.df<-as.data.frame(cbind(mf,ik.10,ik.50))
head(ik.df)
#          x       y WELL_TYPE  As    Fe ik.10 ik.50
# 1 509574.3 2474006       DTW 0.5 0.103 FALSE FALSE
# 2 439962.9 2647931       STW 0.5 0.087 FALSE FALSE
# 3 662328.1 2718502       STW 0.5  1.37 FALSE FALSE
# 4 619708.4 2631583       STW 0.5 0.128 FALSE FALSE
# 5 454332.2 2522667       DTW 0.5 0.019 FALSE FALSE
# 6 438852.0 2576967       STW 0.5 0.042 FALSE FALSE

coordinates(ik.df)=~x+y
coordinates(grid) = ~x+y

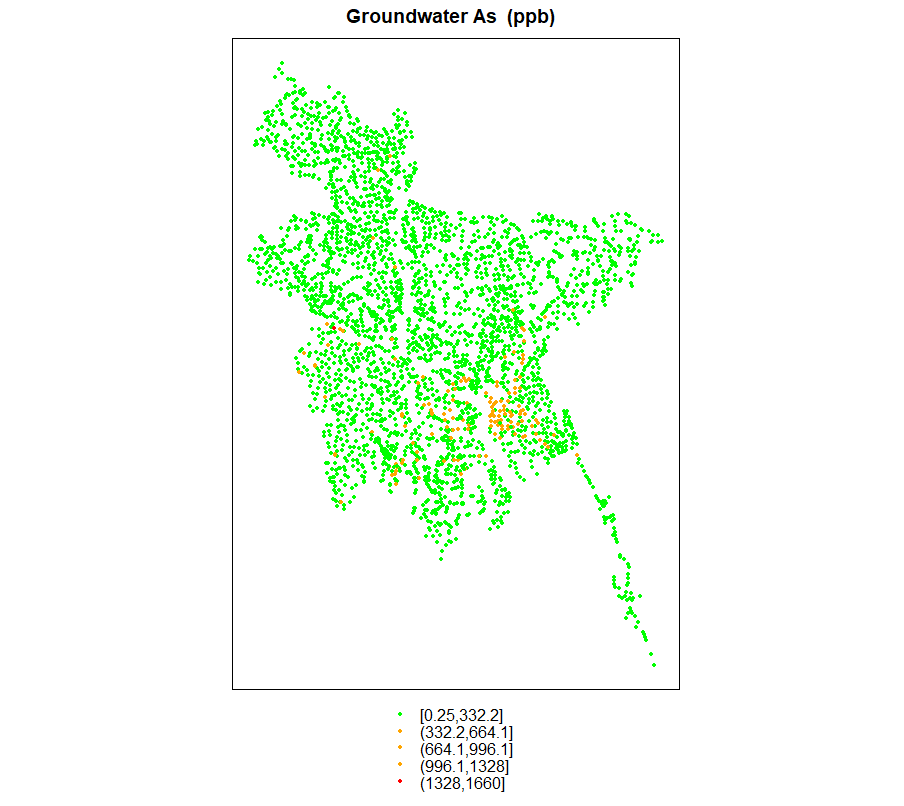
地图数据

  
spplot(ik.df, zcol = "As", col.regions = c("green", "orange", "red"), cex=.5,
       main = "Groundwater As  (ppb)")

  
p1<-spplot(ik.df, zcol = "ik.50", col.regions = c("green", "red"), cex=.5,
       main = "As > 10 ppb")
p2<-spplot(ik.df, zcol = "ik.50", col.regions = c("green", "red"), cex=.5,
       main = " As > 50 ppb")
grid.arrange(p1, p2, ncol=2)

指示变异函数

  
ik.df <- ik.df[-zerodist(ik.df)[,1],] 
# Variogram
v10<-variogram(ik.10~ 1, data = ik.df)
v50<-variogram(ik.50~ 1, data = ik.df)
# Intial parameter set by eye esitmation
m10<-vgm(0.15,"Exp",40000,0.05)
m50<-vgm(0.15,"Exp",40000,0.05)
# least square fit
m.f.10<-fit.variogram(v10, m10)
m.f.50<-fit.variogram(v50, m50)
m.f.10
#   model     psill    range
# 1   Nug 0.1346799     0.00
# 2   Exp 0.1155823 46860.32
m.f.50
#   model     psill    range
# 1   Nug 0.1005604     0.00
# 2   Exp 0.1030162 56236.76

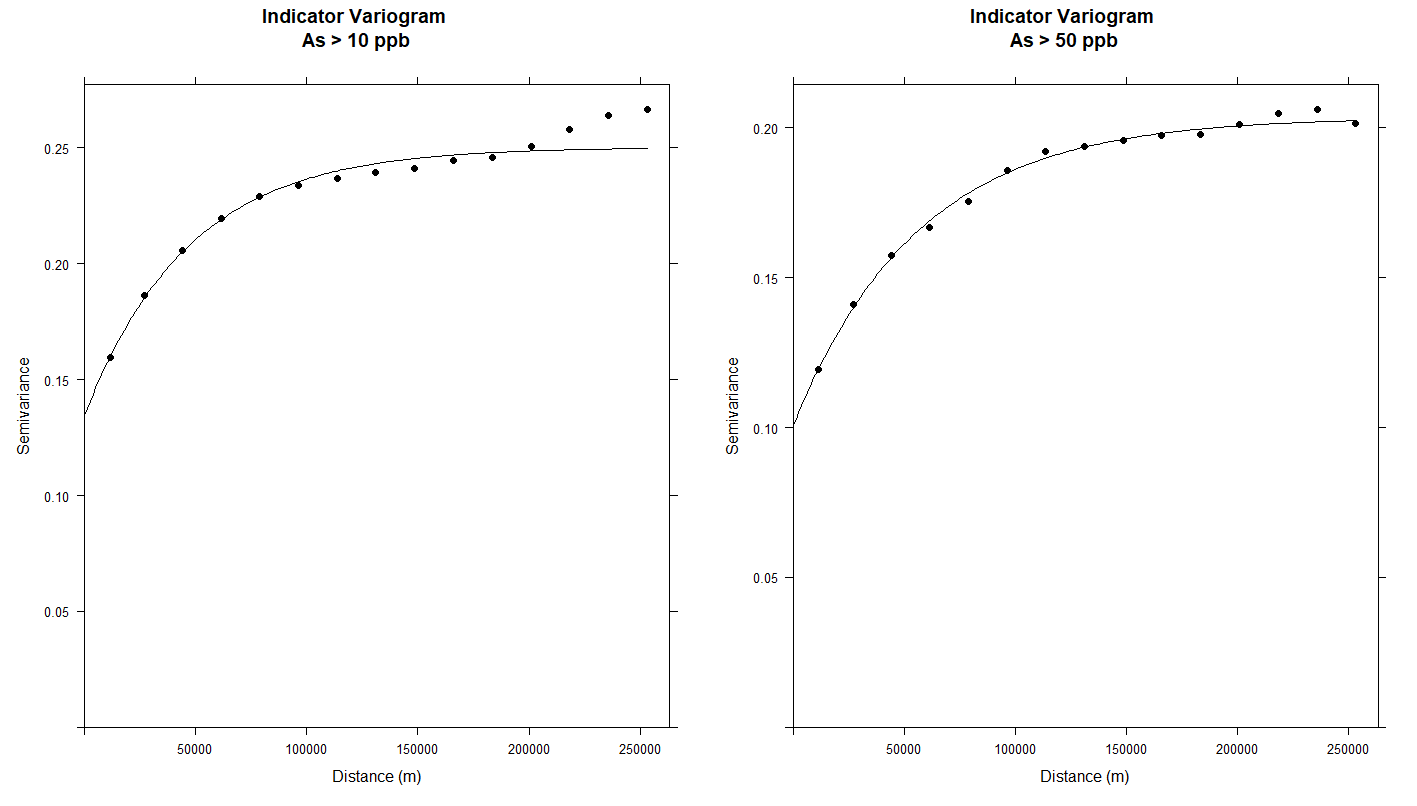
绘制变量图和拟合模型

  
#### Plot varigram and fitted model:
v1<-plot(v10, pl=F, 
     model=m.f.10,
     col="black", 
     cex=0.9, 
     lwd=0.5,
     lty=1,
     pch=19,
     main="Indicator Variogram\n As > 10 ppb",
     xlab="Distance (m)",
     ylab="Semivariance")

v2<-plot(v50, pl=F, 
     model=m.f.50,
     col="black", 
     cex=0.9, 
     lwd=0.5,
     lty=1,
     pch=19,
     main="Indicator Variogram\n As > 50 ppb",
     xlab="Distance (m)",
     ylab="Semivariance")
grid.arrange(v1, v2, nrow = 1)

交叉验证

我们将计算As浓度大于10和5 ppb的IK预测的留一交叉验证 (LOOCV)。它的工作原理与参数克里金法相同: 保持一个点，从其他点预测其真实指标的概率，然后将该概率与指标的实际值进行比较。

  
cv.10 <- krige.cv(ik.10 ~ 1, loc = ik.df, model = m.f.10, nfold=5)
cv.50 <- krige.cv(ik.50 ~ 1, loc = ik.df, model = m.f.50, nfold=5)

将预测概率限制在以下范围内:

  
cv.10$var1.pred <- pmin(1, cv.10$var1.pred)
cv.10$var1.pred <- pmax(0, cv.10$var1.pred)

cv.50$var1.pred <- pmin(1, cv.50$var1.pred)
cv.50$var1.pred <- pmax(0, cv.50$var1.pred)
summary(cv.50)
# Object of class SpatialPointsDataFrame
# Coordinates:
#         min       max
# x  306178.9  751030.6
# y 2298326.2 2946787.5
# Is projected: NA 
# proj4string : [NA]
# Number of points: 3420
# Data attributes:
#    var1.pred          var1.var       observed          residual       
#  Min.   :0.00000   Min.   :0.1081   Mode :logical   Min.   :-0.98272  
#  1st Qu.:0.02597   1st Qu.:0.1158   FALSE:2558      1st Qu.:-0.16356  
#  Median :0.14422   Median :0.1174   TRUE :862       Median :-0.02653  
#  Mean   :0.25246   Mean   :0.1179                   Mean   :-0.00009  
#  3rd Qu.:0.39524   3rd Qu.:0.1193                   3rd Qu.: 0.01103  
#  Max.   :1.00000   Max.   :0.1620                   Max.   : 1.00756  
#      zscore                fold      
#  Min.   :-2.8676192   Min.   :1.000  
#  1st Qu.:-0.4769934   1st Qu.:2.000  
#  Median :-0.0766899   Median :3.000  
#  Mean   :-0.0001732   Mean   :3.034  
#  3rd Qu.: 0.0320861   3rd Qu.:4.000  
#  Max.   : 2.9818489   Max.   :5.000  

  
summary(cv.10)
# Object of class SpatialPointsDataFrame
# Coordinates:
#         min       max
# x  306178.9  751030.6
# y 2298326.2 2946787.5
# Is projected: NA 
# proj4string : [NA]
# Number of points: 3420
# Data attributes:
#    var1.pred         var1.var       observed          residual         
#  Min.   :0.0000   Min.   :0.1447   Mode :logical   Min.   :-0.9972481  
#  1st Qu.:0.1316   1st Qu.:0.1550   FALSE:1978      1st Qu.:-0.2416887  
#  Median :0.3980   Median :0.1572   TRUE :1442      Median :-0.0203483  
#  Mean   :0.4217   Mean   :0.1577                   Mean   : 0.0000371  
#  3rd Qu.:0.6899   3rd Qu.:0.1596                   3rd Qu.: 0.2491982  
#  Max.   :1.0000   Max.   :0.2119                   Max.   : 1.0037231  
#      zscore                fold      
#  Min.   :-2.5405964   Min.   :1.000  
#  1st Qu.:-0.6123220   1st Qu.:2.000  
#  Median :-0.0512903   Median :3.000  
#  Mean   : 0.0001323   Mean   :3.008  
#  3rd Qu.: 0.6276619   3rd Qu.:4.000  
#  Max.   : 2.5629406   Max.   :5.000 

现在，我们将制作预测概率的后置图，符号大小与概率成比例，红色的点表示假指标，绿色的点表示真指标

  
par(mfrow=c(1,2))
plot(coordinates(cv.10), asp = 1, pch=21, col = ifelse(cv.10$observed,
 "red", "green"), cex = 0.2 + 1 * cv.10$var1.pred,
 xlab = "E (km)", ylab = "N (km)", main = "Probability of TRUE indicator (10 ppb)",
 sub = "Actual indicator: green/red = FALSE/TRUE")
 grid()

plot(coordinates(cv.50), asp = 1, pch=21, col = ifelse(cv.50$observed,
 "red", "green"), cex = 0.4 + 1 * cv.50$var1.pred,
 xlab = "E (km)", ylab = "N (km)", main = "Probability of TRUE indicator (50 ppb)",
 sub = "Actual indicator: green/red = FALSE/TRUE")
 grid()

par(mfrow=c(1,1))

网格位置的 IK 预测

  
ik.grid.10<-krige(ik.10~ 1, nmax=50,
              loc=ik.df,        # Data frame
              newdata=grid,     # Prediction location
              model = m.f.10)   # fitted varigram model
# [using ordinary kriging]
ik.grid.50<-krige(ik.50~ 1, nmax=50,
              loc=ik.df,        # Data frame
              newdata=grid,     # Prediction location
              model = m.f.50)   # fitted varigram model 
# [using ordinary kriging]

  
summary(ik.grid.50)
# Object of class SpatialPointsDataFrame
# Coordinates:
#         min       max
# x  301021.7  751021.7
# y 2279492.7 2944492.7
# Is projected: NA 
# proj4string : [NA]
# Number of points: 5339
# Data attributes:
#    var1.pred            var1.var     
#  Min.   :-0.005204   Min.   :0.1084  
#  1st Qu.: 0.014550   1st Qu.:0.1150  
#  Median : 0.129556   Median :0.1167  
#  Mean   : 0.237453   Mean   :0.1197  
#  3rd Qu.: 0.378431   3rd Qu.:0.1198  
#  Max.   : 1.000370   Max.   :0.1883

summary(ik.grid.10)
# Object of class SpatialPointsDataFrame
# Coordinates:
#         min       max
# x  301021.7  751021.7
# y 2279492.7 2944492.7
# Is projected: NA 
# proj4string : [NA]
# Number of points: 5339
# Data attributes:
#    var1.pred            var1.var     
#  Min.   :-0.006402   Min.   :0.1451  
#  1st Qu.: 0.097765   1st Qu.:0.1541  
#  Median : 0.368668   Median :0.1564  
#  Mean   : 0.407622   Mean   :0.1601  
#  3rd Qu.: 0.684044   3rd Qu.:0.1604  
#  Max.   : 1.000148   Max.   :0.2436  

将预测概率限制在以下范围内:

  
ik.grid.10$var1.pred <- pmin(1, ik.grid.10$var1.pred)
ik.grid.10$var1.pred <- pmax(0, ik.grid.10$var1.pred)

ik.grid.50$var1.pred <- pmin(1, ik.grid.50$var1.pred)
ik.grid.50$var1.pred <- pmax(0, ik.grid.50$var1.pred)
summary(ik.grid.50)
# Object of class SpatialPointsDataFrame
# Coordinates:
#         min       max
# x  301021.7  751021.7
# y 2279492.7 2944492.7
# Is projected: NA 
# proj4string : [NA]
# Number of points: 5339
# Data attributes:
#    var1.pred          var1.var     
#  Min.   :0.00000   Min.   :0.1084  
#  1st Qu.:0.01455   1st Qu.:0.1150  
#  Median :0.12956   Median :0.1167  
#  Mean   :0.23748   Mean   :0.1197  
#  3rd Qu.:0.37843   3rd Qu.:0.1198  
#  Max.   :1.00000   Max.   :0.1883  

summary(ik.grid.10)
# Object of class SpatialPointsDataFrame
# Coordinates:
#         min       max
# x  301021.7  751021.7
# y 2279492.7 2944492.7
# Is projected: NA 
# proj4string : [NA]
# Number of points: 5339
# Data attributes:
#    var1.pred          var1.var     
#  Min.   :0.00000   Min.   :0.1451  
#  1st Qu.:0.09777   1st Qu.:0.1541  
#  Median :0.36867   Median :0.1564  
#  Mean   :0.40764   Mean   :0.1601  
#  3rd Qu.:0.68404   3rd Qu.:0.1604  
#  Max.   :1.00000   Max.   :0.2436  

转换为栅格

  
p10<-rasterFromXYZ(as.data.frame(ik.grid.10)[, c("x", "y", "var1.pred")])
p50<-rasterFromXYZ(as.data.frame(ik.grid.50)[, c("x", "y", "var1.pred")])

绘制概率图

为了绘制地图，我们将使用 rasterVis 包的 levelplot() 函数。

  
colr <-  colorRampPalette(c("blue","green",'yellow',"red"), space = "rgb")
p.strip <- list(cex=1.25)
ckey <- list(labels=list(cex=1, rot=0), height=1)

ik.plot.10<-levelplot(p10, 
             margin=FALSE, 
             auto.key=FALSE,
             scales=list(y=list(draw=F,cex=.3,rot=90, tck= 0.35,alternating=1,col="grey"),
             x=list(draw=F, cex=.3,tck= .35)),
             par.settings=list(axis.line=list(col='grey')), 
             col.regions=colr, 
             colorkey=ckey, 
             par.strip.text=p.strip,
             main="Probability As > 10 ppb")

ik.plot.50<-levelplot(p50, 
             margin=FALSE, 
             auto.key=FALSE,
             scales=list(y=list(draw=F,cex=.3,rot=90, tck= 0.35,alternating=1,col="grey"),
             x=list(draw=F, cex=.3,tck= .35)),
             par.settings=list(axis.line=list(col='grey')), 
             col.regions=colr, 
             colorkey=ckey, 
             par.strip.text=p.strip,
             main="Probability As > 50 ppb")

grid.arrange(ik.plot.10, ik.plot.50, nrow = 1)

R, Spatial Interpolate

This post is licensed under CC BY 4.0 by the author.

半变异函数建模

加载包和数据

实验变异函数

变异函数云图

各向同性变异函数

各向异性变异函数

变异函数图

方向变异函数

拟合变异函数模型

指数 (Exp) 模型

球面(Sph)模型

拟合优度

用变换后的数据进行变异函数建模

Log10转换

幂变换 (Box-Cox)

嵌套模型拟合

短程结构

远程结构

克里金插值

普通克里金

加载包和数据

数据变换

变异函数建模

绘制变量图和拟合模型

点或准时克里金法

逆变换

转换为栅格

绘制预测 SOC 和 OK 误差

块克里金法

逆变换

转换为栅格

绘图

泛克里金

数据变换

变异函数建模

绘制残差方差图和拟合模型

克里金预测

逆变换

转换为栅格

绘制预测 SOC 和 UK 误差

协同克里金

幂变换

相关矩阵

协区域化或 Corss-Varoigram 的变异函数模型

目标变量直接方差图（SOC）

协变量变异函数建模的直接变异函数(NDVI)

交叉变异函数

网格位置的协同克里金法预测

逆变换

转换为栅格

绘制预测 SOC 和 CK 误差

回归克里金

幂变换

创建 dataframes

开始foreach并行化以进行模型拟合

设置控制参数

广义线性模型

拟合广义线性模型 (GLM)

GLM 残差的变异函数建模

网格位置的GLM预测

克里金法预测 (SK + 回归预测)

逆变换

转换为栅格

绘制预测 SOC

随机森林

拟合随机森林模型 (RF)

RF 残差的变异函数建模

网格位置的预测

克里金法预测 (SK + 回归)

逆变换

转换为栅格

绘制预测 SOC

元集成机器学习

创建模型列表

拟合所有模型

子模型的性能

绘制 K 折交叉验证结果 (MAE，RMSE，R2)

通过叠加来组合几个预测模型

集合结果

残差的变异函数建模