空间插值预测质量评估【R】

Posted Feb 23, 2023 Updated Oct 6, 2023

By renkaigis 18 min read

空间插值或预测模型的准确性至关重要，因为它决定了插值值的质量。与空间预测的准确性评估相比，开发空间预测模型要容易得多，但是通常情况下，空间预测模型仍然未知。

空间预测质量的评价措施是: 具有 kriging 方差的残差的平均误差 (ME)，平均绝对误差 (MAE)，均方根误差 (RMSE) 和 均方偏差比 (MSDR) ，可以计算为:

在本练习中，我们将使用以下三种方法评估普通克里金法预测的质量:

交叉验证
使用独立数据集进行验证
空间不确定性的条件模拟

原文链接：Geospatial Data Science with R

全部机翻，如有错误，以你的感觉为准。

交叉验证

交叉验证是一种重新抽样的过程，用于在有限的数据样本上评估模型。它优于残差评价。两种主要的交叉验证技术通常用于模型评估: 1) K-fold 交叉验证（K-fold cross validation）； 2)留一交叉验证（Leave-one-out cross validation）。

在 K 折交叉验证中，将数据集随机分为测试集和训练集 k 个不同的时间，并重复进行模型进化 k 次。每次，将 k 个子集中的一个作为测试集，将其他 k-1 子集放在一起形成训练集。然后计算所有 k 个试验的平均误差。该方法的一种变体是将数据随机分为 k 个不同时间的测试和训练集。

在留一交叉验证中，K 等于 N，集合中的数据点的数量。对除一个点以外的所有数据训练模型，并对该点进行预测。最终，使用所有其他观测值分别在每个观测点进行模型预测，并计算平均误差并将其用于评估模型。

  
library(plyr)
library(dplyr)
library(gstat)
library(raster)
library(ggplot2)
library(car)
library(classInt)
library(RStoolbox)
library(spatstat)
library(dismo)
library(fields)
library(gridExtra)

# Define data folder
dataFolder<-"D:\\Env\\DATA_08\\"
train<-read.csv(paste0(dataFolder,"train_data.csv"), header= TRUE) 

数据变换

幂变换使用 Box和Cox (1964) 的最大似然方法来选择针对正态性的单变量或多变量响应的变换。首先，我们必须使用 car 包的 powerTransform() 函数计算适当的转换参数，然后使用此参数使用 bcPower() 函数对数据进行转换。

  
powerTransform(train$SOC)
# Estimated transformation parameter 
# train$SOC 
# 0.2523339 
train$SOC.bc<-bcPower(train$SOC, 0.2523339)

coordinates(train) = ~x+y

变异函数建模

  
# Variogram
v<-variogram(SOC.bc~ 1, data = train, cloud=F)
# Intial parameter set by eye esitmation
m<-vgm(1.5,"Exp",40000,0.5)
# least square fit
m.f<-fit.variogram(v, m)
m.f
#   model     psill    range
# 1   Nug 0.5165678     0.00
# 2   Exp 1.0816886 82374.23

K-fold 交叉验证

我们将使用 k-fold 交叉验证对模型进行评估。我们将使用 krige.cv() 函数。

  
cv<-krige.cv(SOC.bc ~ 1,
         train,              # data
         model = m.f,        # fitted varigram model 
         nfold=10)           # five-fold cross validation
summary(cv)
# Object of class SpatialPointsDataFrame
# Coordinates:
#        min        max
# x -1246454   83927.82
# y  1019863 2526240.55
# Is projected: NA 
# proj4string : [NA]
# Number of points: 368
# Data attributes:
#    var1.pred         var1.var         observed         residual        
#  Min.   :0.1761   Min.   :0.8063   Min.   :-1.499   Min.   :-3.188626  
#  1st Qu.:1.4505   1st Qu.:0.9752   1st Qu.: 1.149   1st Qu.:-0.721998  
#  Median :2.0100   Median :1.0540   Median : 1.974   Median :-0.056187  
#  Mean   :1.9901   Mean   :1.0600   Mean   : 1.981   Mean   :-0.008895  
#  3rd Qu.:2.5575   3rd Qu.:1.1274   3rd Qu.: 2.919   3rd Qu.: 0.713665  
#  Max.   :3.9450   Max.   :1.4779   Max.   : 5.423   Max.   : 2.936493  
#      zscore               fold       
#  Min.   :-3.286167   Min.   : 1.000  
#  1st Qu.:-0.687623   1st Qu.: 3.000  
#  Median :-0.055530   Median : 6.000  
#  Mean   :-0.007057   Mean   : 5.639  
#  3rd Qu.: 0.693822   3rd Qu.: 8.000  
#  Max.   : 2.994699   Max.   :10.000  

残差图

  
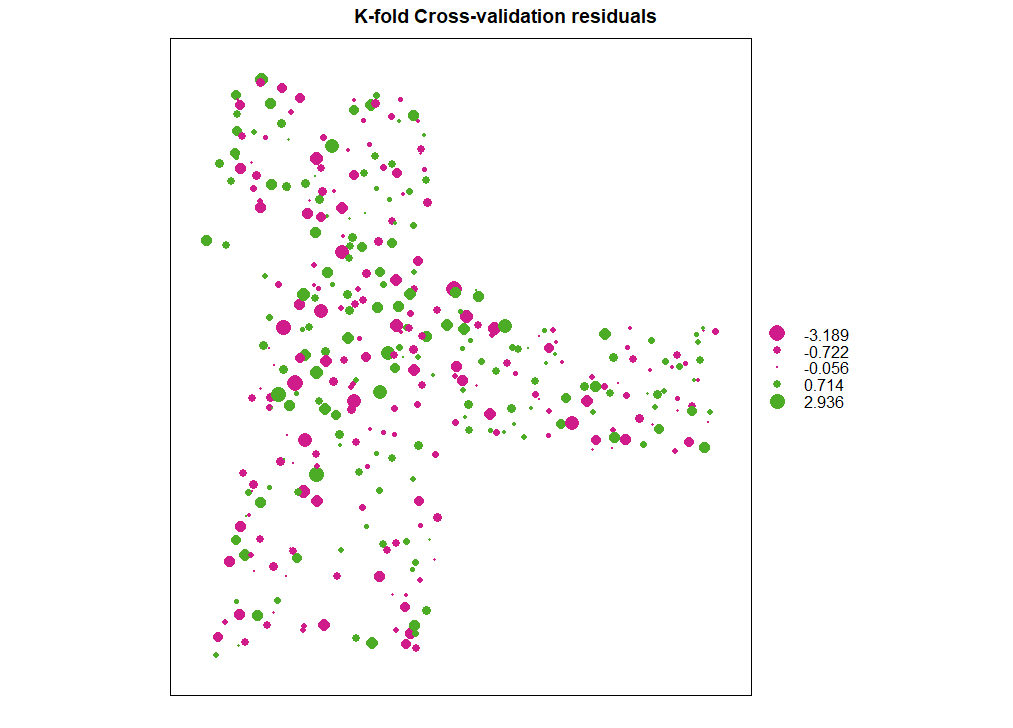
bubble(cv, zcol = "residual", maxsize = 2.0,  main = "K-fold Cross-validation residuals")

  
# Mean Error (ME)
ME<-round(mean(cv$residual),3)
# Mean Absolute Error
MAE<-round(mean(abs(cv$residual)),3)
# Root Mean Squre Error (RMSE)
RMSE<-round(sqrt(mean(cv$residual^2)),3)
# Mean Squared Deviation Ratio (MSDR)
MSDR<-mean(cv$residual^2/cv$var1.var)

ME
# [1] -0.009
MAE
# [1] 0.826
RMSE
# [1] 1.04
MSDR
# [1] 1.03143

实际值 vs 预测值: 线性回归

比较实际值与预测值的另一种方法是在它们之间进行线性回归。理想情况下，这将是一条1:1 的线: 截距为 0 (无偏差)，斜率设置为 1 (增益相等)。

  
lm.cv <- lm(cv$var1.pred ~ cv$observed)
summary(lm.cv)
# Call:
# lm(formula = cv$var1.pred ~ cv$observed)

# Residuals:
#      Min       1Q   Median       3Q      Max 
# -1.70179 -0.40920 -0.03429  0.44986  2.20694 

# Coefficients:
#             Estimate Std. Error t value Pr(>|t|)    
# (Intercept)   1.2902     0.0602   21.43   <2e-16 ***
# cv$observed   0.3533     0.0255   13.85   <2e-16 ***
# ---
# Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

# Residual standard error: 0.6279 on 366 degrees of freedom
# Multiple R-squared:  0.3439,	Adjusted R-squared:  0.3422 
# F-statistic: 191.9 on 1 and 366 DF,  p-value: < 2.2e-16

1:1 绘图

  
par(mfrow=c(1,1))

留一交叉验证

  
cv.LOOCV<-krige.cv(SOC.bc ~ 1,
         train,           # data
         model = m.f)    # fitted varigram model 
summary(cv.LOOCV)
# Object of class SpatialPointsDataFrame
# Coordinates:
#        min        max
# x -1246454   83927.82
# y  1019863 2526240.55
# Is projected: NA 
# proj4string : [NA]
# Number of points: 368
# Data attributes:
#    var1.pred         var1.var         observed         residual        
#  Min.   :0.1107   Min.   :0.8041   Min.   :-1.499   Min.   :-3.188887  
#  1st Qu.:1.4400   1st Qu.:0.9591   1st Qu.: 1.149   1st Qu.:-0.708533  
#  Median :1.9942   Median :1.0281   Median : 1.974   Median :-0.008027  
#  Mean   :1.9824   Mean   :1.0382   Mean   : 1.981   Mean   :-0.001238  
#  3rd Qu.:2.5319   3rd Qu.:1.1016   3rd Qu.: 2.919   3rd Qu.: 0.723783  
#  Max.   :3.9177   Max.   :1.4022   Max.   : 5.423   Max.   : 2.934362  
#      zscore               fold       
#  Min.   :-3.286447   Min.   :  1.00  
#  1st Qu.:-0.698335   1st Qu.: 92.75  
#  Median :-0.008109   Median :184.50  
#  Mean   :-0.000655   Mean   :184.50  
#  3rd Qu.: 0.721153   3rd Qu.:276.25  
#  Max.   : 2.992528   Max.   :368.00 

  
# Mean Error (ME)
ME.LOOCV<-round(mean(cv.LOOCV$residual),3)
# Mean Absolute Error
MAE.LOOCV<-round(mean(abs(cv.LOOCV$residual)),3)
# Root Mean Squre Error (RMSE)
RMSE.LOOCV<-round(sqrt(mean(cv.LOOCV$residual^2)),3)
# Mean Squared Deviation Ratio (MSDR)
MSDR.LOOCV<-mean(cv.LOOCV$residual^2/cv$var1.var)

ME.LOOCV
# [1] -0.001
MAE.LOOCV
# [1] 0.832
RMSE.LOOCV
# [1] 1.042
MSDR.LOOCV
# [1] 1.033859

使用独立数据集进行验证

本节我们使用 89 个测试位置的 SOC 数据来验证来自 386 训练数据的普通 kriging 预测。由于我们不会使用测试数据集的 89 点来拟合模型或预测，因此这些都是对模型的独立测试。我们可以将预测值与实际值进行比较。

  
library(plyr)
library(dplyr)
library(gstat)
library(raster)
library(ggplot2)
library(car)
library(classInt)
library(RStoolbox)
library(spatstat)
library(dismo)
library(fields)
library(gridExtra)

# Define data folder
dataFolder<-"D:\\Env\\DATA_08\\"
train<-read.csv(paste0(dataFolder,"train_data.csv"), header= TRUE) 
test<-read.csv(paste0(dataFolder,"test_data.csv"), header= TRUE) 

数据变换-幂变换

  
powerTransform(train$SOC)
# Estimated transformation parameter 
# train$SOC 
# 0.2523339 

powerTransform(test$SOC)
# Estimated transformation parameter 
#  test$SOC 
# 0.3379903

train$SOC.bc<-bcPower(train$SOC, 0.2523339)
test$SOC.bc<-bcPower(test$SOC, 0.3379903)

  
coordinates(train) = ~x+y
coordinates(test) = ~x+y

变异函数建模

  
# Variogram
v<-variogram(SOC.bc~ 1, data = train, cloud=F)
# Intial parameter set by eye esitmation
m<-vgm(1.5,"Exp",40000,0.5)
# least square fit
m.f<-fit.variogram(v, m)
m.f
#   model     psill    range
# 1   Nug 0.5165678     0.00
# 2   Exp 1.0816886 82374.23

测试点的预测

我们将使用 k-fold 交叉验证对模型进行评估。我们将使用 krige.cv() 函数。

  
val<-krige(SOC.bc ~ 1,
         train,        
         test,
         model = m.f)
# [using ordinary kriging]

summary(val)
# Object of class SpatialPointsDataFrame
# Coordinates:
#        min        max
# x -1185457   95251.19
# y  1102846 2514145.42
# Is projected: NA 
# proj4string : [NA]
# Number of points: 101
# Data attributes:
#    var1.pred         var1.var     
#  Min.   :0.1426   Min.   :0.7888  
#  1st Qu.:1.3910   1st Qu.:0.9471  
#  Median :1.8303   Median :1.0099  
#  Mean   :1.9214   Mean   :1.0212  
#  3rd Qu.:2.4667   3rd Qu.:1.0756  
#  Max.   :3.8089   Max.   :1.3132 

计算残差

  
test$SOC.pred<-val$var1.pred
test$SOC.var<-val$var1.var
test$residual<-(test$SOC.bc-test$SOC.pred)

残差图

  
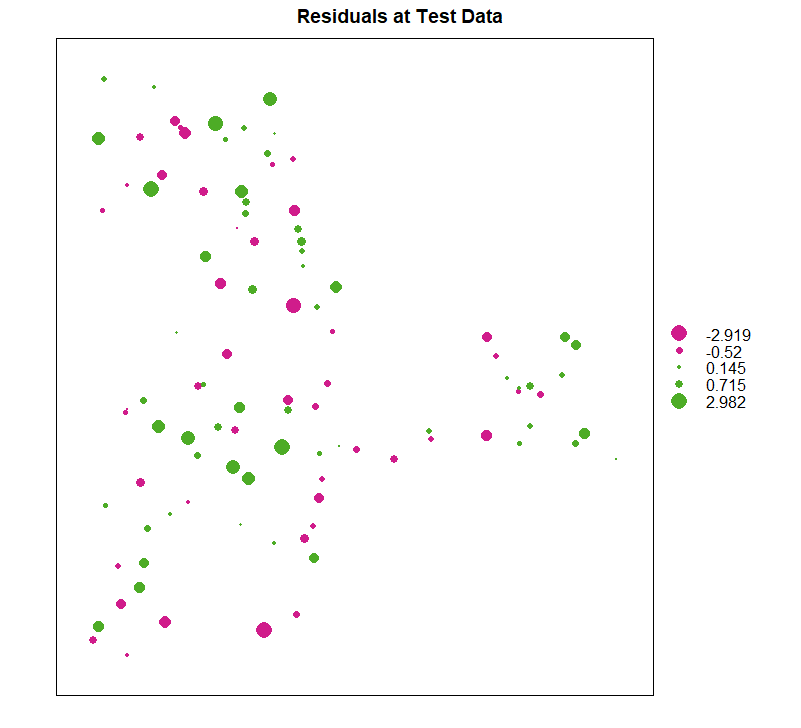
bubble(test, zcol = "residual", maxsize = 2.0,  main = "Residuals at Test Data")

误差

  
# Mean Error (ME)
ME<-round(mean(test$residual),3)
# Mean Absolute Error
MAE<-round(mean(abs(test$residual)),3)
# Root Mean Squre Error (RMSE)
RMSE<-round(sqrt(mean(test$residual^2)),3)
# Mean Squared Deviation Ratio (MSDR)
MSDR<-mean(test$residual^2/test$SOC.var)

ME
# [1] 0.152
MAE
# [1] 0.873
RMSE
# [1] 1.126
MSDR
# [1] 1.267439

实际值 vs 预测值: 线性回归

比较实际值与预测值的另一种方法是在它们之间进行线性回归。理想情况下，这将是一条1:1 的线: 截距为0 (无偏差)，斜率设置为1 (增益相等)。

  
lm.val <- lm(test$SOC.pred ~ test$SOC.bc)
summary(lm.val)
# Call:
# lm(formula = test$SOC.pred ~ test$SOC.bc)

# Residuals:
#      Min       1Q   Median       3Q      Max 
# -1.16895 -0.42721  0.07515  0.28345  1.30121 

# Coefficients:
#             Estimate Std. Error t value Pr(>|t|)    
# (Intercept)  1.19921    0.09196  13.041  < 2e-16 ***
# test$SOC.bc  0.34824    0.03592   9.695 5.07e-16 ***
# ---
# Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

# Residual standard error: 0.5419 on 99 degrees of freedom
# Multiple R-squared:  0.487,	Adjusted R-squared:  0.4818 
# F-statistic: 93.99 on 1 and 99 DF,  p-value: 5.069e-16

1:1 图

  
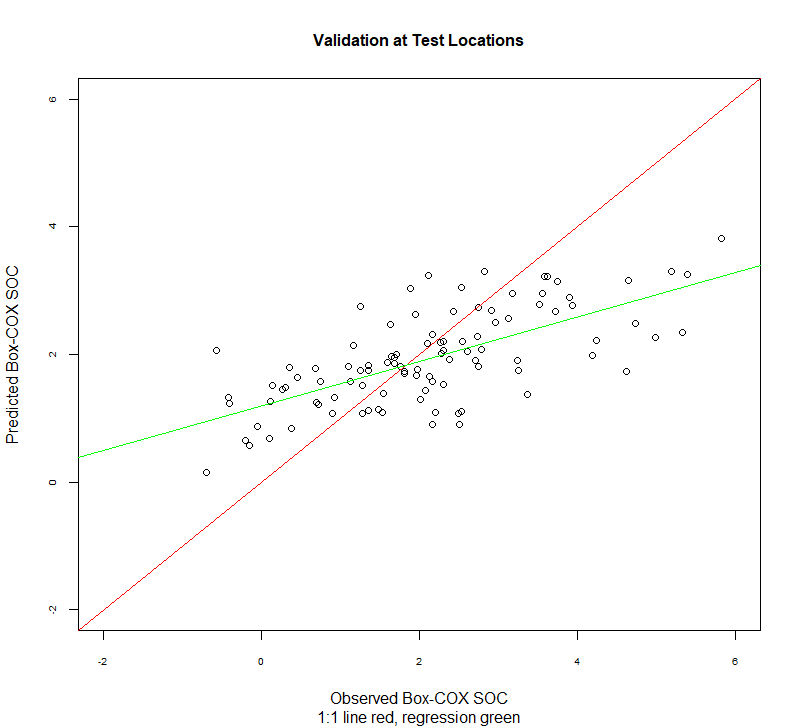
plot(test$SOC.bc, test$SOC.pred,main=list("Validation at Test Locations",cex=1),
   sub = "1:1 line red, regression green",
   xlab = "Observed Box-COX SOC",
   ylab = "Predicted Box-COX SOC", 
   cex.axis=.6,
   xlim = c(-2,6), 
   ylim =c(-2,6), 
   pch = 21, 
   cex=1)
abline(0, 1, col="red")
abline(lm.val, col = "green")

空间不确定性的条件模拟

该 kriging 预测图平滑了所研究属性的空间分布的局部细节，小值被高估，而大值被低估，尤其是在低采样密度的区域 (Isaaks和Srivastava 1989)。与kriging不同，条件顺序高斯模拟 (CSGS) 技术可以更好地反映现实，并消除不切实际的平滑，除了尊重原始数据值外，还着重于全局统计数据或半变异函数模型的再现 (Goovaerts 1997)。使用 csg 生成的一组替代实现提供了有关空间预测的一定程度的不确定性，该不确定性通常用于绘制所研究变量的可靠概率图 (Goovaerts 1997)。因此，csg越来越优选用于表征决策和风险分析的不确定性的 kriging，而不是像使用 kriging (Deutsch和Journel 1998) 那样产生未采样位置的最佳无偏预测。

  
library(plyr)
library(dplyr)
library(gstat)
library(raster)
library(rasterVis)
library(ggplot2)
library(car)
library(sp)
library(classInt)
library(RStoolbox)
library(gridExtra)

dataFolder<-"D:\\Env\\DATA_08\\"
state<-shapefile(paste0(dataFolder,"GP_STATE.shp"))
train<-read.csv(paste0(dataFolder,"train_data.csv"), header= TRUE) 
grid<-read.csv(paste0(dataFolder, "GP_prediction_grid_data.csv"), header= TRUE)
grid.xy<-grid[,1:3]

数据变换-幂变换

  
powerTransform(train$SOC)
train$SOC.bc<-bcPower(train$SOC, 0.2523339)
coordinates(train) = ~x+y
coordinates(grid) = ~x+y

变异函数建模

  
# Variogram
v<-variogram(SOC.bc~ 1, data = train, cloud=F)
# Intial parameter set by eye esitmation
m<-vgm(1.5,"Exp",40000,0.5)
# least square fit
m.f<-fit.variogram(v, m)
m.f
#   model     psill    range
# 1   Nug 0.5165678     0.00
# 2   Exp 1.0816886 82374.23

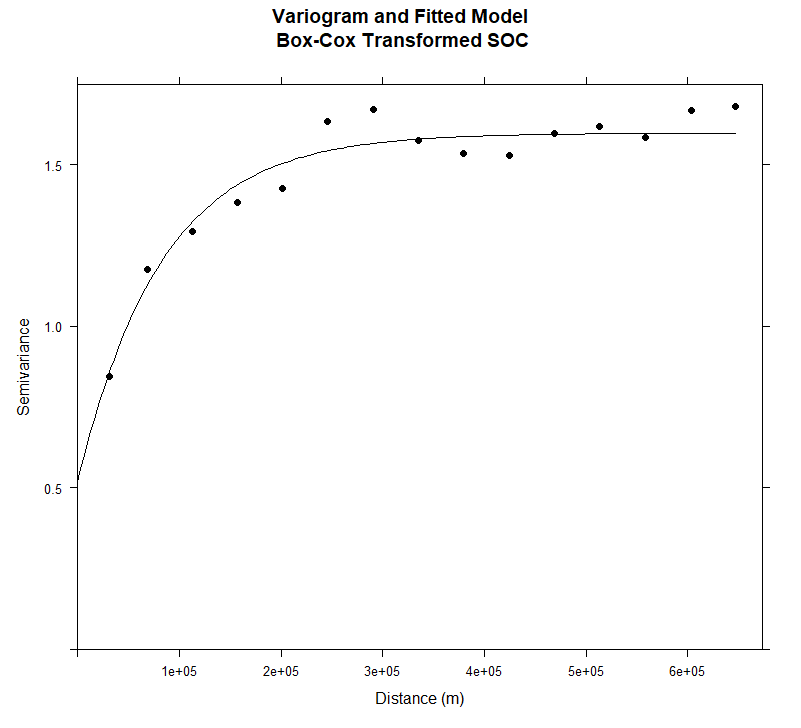
绘制变量图和拟合模型

  
#### Plot varigram and fitted model:
plot(v, pl=F, 
     model=m.f,
     col="black", 
     cex=0.9, 
     lwd=0.5,
     lty=1,
     pch=19,
     main="Variogram and Fitted Model\n Box-Cox Transformed SOC",
     xlab="Distance (m)",
     ylab="Semivariance")

普通克里金

  
ok.soc<-krige(SOC.bc~1, 
              train, 
              grid,
              model=m.f, 
              nmax=50
              )

# back transformation
k1<-1/0.2523339                                   
grid.xy$OK <-((ok.soc$var1.pred *0.2523339+1)^k1)

条件高斯模拟

krige() 方法也可以做条件模拟。它需要一个可选的参数: nsim ，条件模拟的数量

  
set.seed(130)
nsim=100
sim.soc<-krige(SOC.bc~1, 
              train, 
              grid,
              model=m.f, 
              nmax=50, 
              nsim = nsim)
# drawing 100 GLS realisations of beta...
# [using conditional Gaussian simulation]

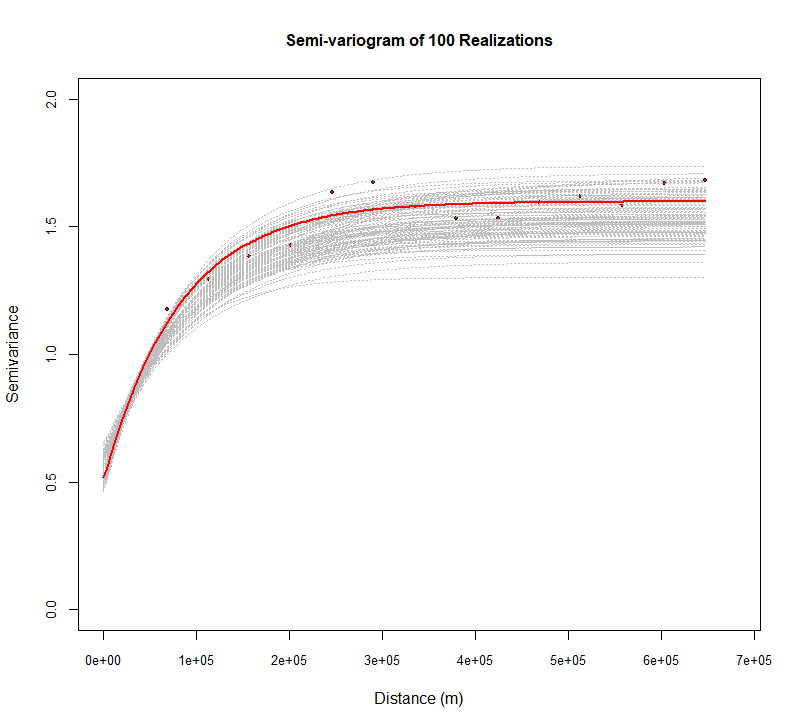
所有实现的半真实图

模拟应该尊重空间结构-与变异函数模型相同的结构。现在将产生 100 实现的变量，并绘制box-cox变换 SOC 的变量。

  
plot(v$gamma ~ v$dist, xlim = c(0, max(v$dist) * 1.05),
ylim=c(0,2),
pch = 19, col = "black",cex=.5,
cex.axis = 0.8, cex.lab=1, xlab = list("Distance (m)",cex=1), ylab =list("Semivariance",cex=1),
main=list("Semi-variogram of 100 Realizations",cex=1))
for(i in 1:100) {
   sg.v=paste("sim",i,sep="")
   fg.v = as.formula(paste(sg.v, "~1"))
   vg.v = variogram(fg.v, sim.soc)
   lines(variogramLine(fit.variogram(vg.v, m.f),
   maxdist = max(v$dist)),lty=3, col = "grey")
}
points(v$gamma ~ v$dist,pch = 19, col = "red",cex=2)
lines(variogramLine(fit.variogram(v,  m.f), 
maxdist = max(v$dist)), col = "red",  lwd=2.0)

逆变换

  
for(i in 1:length(sim.soc@data)){sim.soc@data[[i]] <- (((sim.soc[[i]]*0.2523339+1)^k1))}
sim.data<-as.data.frame(sim.soc)

空间不确定性的可视化

该组实现提供了有关砷浓度空间分布的不确定性的度量。实现之间的差异描述了不确定性。这种不确定性可以通过所有实现的动画显示来可视化，这允许区分在所有实现 (低不确定性) 上保持稳定的区域与在实现之间发生大波动的区域 (高不确定性)。

数据准备

  
soc=sim.data[,3:102]
soc.stack=stack(soc)
# round(quantile(soc.stack$values, probs=seq(0,1, by=.1)),1)
at.soc=classIntervals(soc.stack$values, n = 10, style = "quantile")$brks
rgb.palette <- colorRampPalette(c("red" ,"yellow","green","blue"),space = "rgb")
bound <- list("sp.lines", as(state, "SpatialLines"), col="grey40", lwd=.8,lty=1)
coordinates(sim.data) <- ~x+y
gridded(sim.data) <- TRUE

要在 R 中创建动画地图，您必须在 R 中安装 animation 包。这个包依赖于 ImageMagick 软件。

  
Sys.setenv(PATH = paste("C:\\Program Files\\ImageMagick-7.1.0-Q16-HDRI", Sys.getenv("PATH"), sep = ";"))
# ani.options(convert="C:\\Program Files\\ImageMagick-7.0.6-0-Q16\\covert.exe")
magickPath<-shortPathName("C:\\Program Files\\ImageMagick-7.1.0-Q16-HDRI\\magick.exe")
ani.options(convert=magickPath)

动画地图

  
saveGIF(
for (i in 1:100){
print(spplot(sim.data[,i], main = list(label=paste("Realization",i),cex=1.5),
sp.layout=list(bound),
   par.settings=list(axis.line=list(col="grey25",lwd=0.5)),at=at.soc,
   colorkey=list(space="right",width=1.4,at=1:11,labels=list(cex=1.2,at=1:11,
   labels=c("",   "< 1.2",   "",   " 2.9", "",  " 4.7",  "",  " 7.2", "",  "> 12.5",  ""))),
   col.regions=rgb.palette(20)))}, 
height = 600, width = 600, interval = .5, outdir = getwd())

局部不确定性的度量

现在，我们将通过比较 E-tpye (平均值)，预期 10% 概率的条件 qauntiles图，50% (中位数) 和 90% 来测量局部不确定性。

  
# E-type estimate
df<-as.data.frame(sim.data)
df<-df[,1:100]
grid.xy$mean<-as.data.frame(rowMeans(df[sapply(df, is.numeric)]))
# names(grid.xy)[5]<-"Etype"
## Conditional Quantiles
grid.xy$q10<-apply(as.data.frame(sim.data)[3:102],1,stats::quantile,probs = 0.1,na.rm=TRUE) 
grid.xy$Median<-apply(as.data.frame(sim.data)[3:102],1,stats::quantile,probs = 0.5,na.rm=TRUE)
grid.xy$q90<-apply(as.data.frame(sim.data)[3:102],1,stats::quantile,probs = 0.9,na.rm=TRUE)

  
coordinates(grid.xy) <- ~x+y
gridded(grid.xy) <- TRUE

col <- colorRampPalette(c("red" ,"yellow","green","blue","sky blue"),space = "rgb")
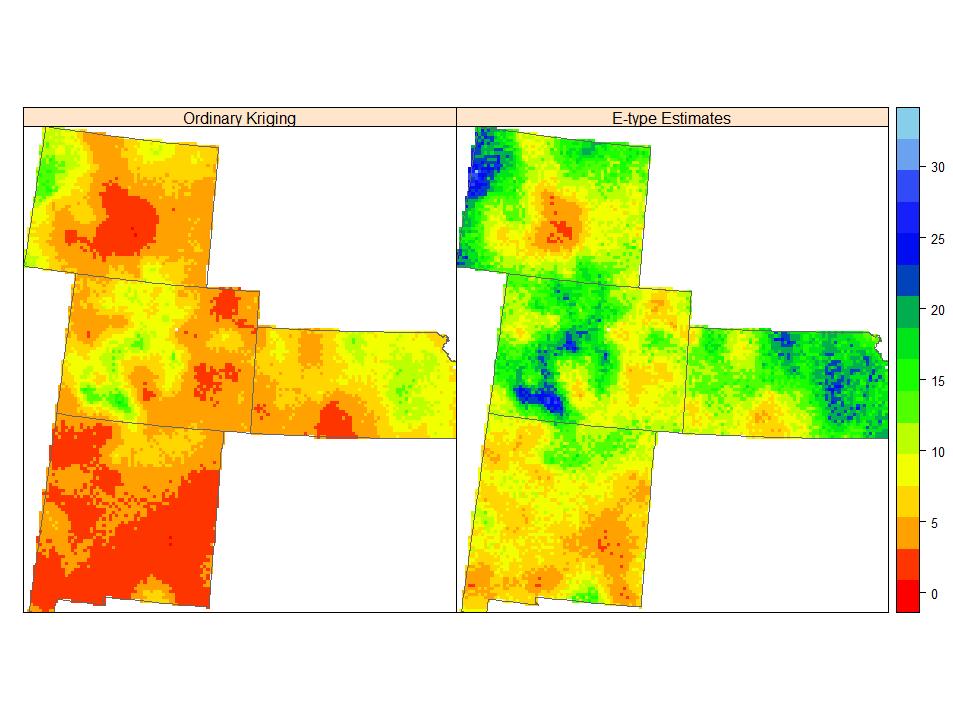
spplot(grid.xy, c(4:5), sp.layout=list(bound), col.regions=col(20),
       names.attr = c("Ordinary Kriging", "E-type Estimates"))

100 实现的普通预测和 E 型估计并不相同，尽管两者都是最小二乘标准的最佳估计。

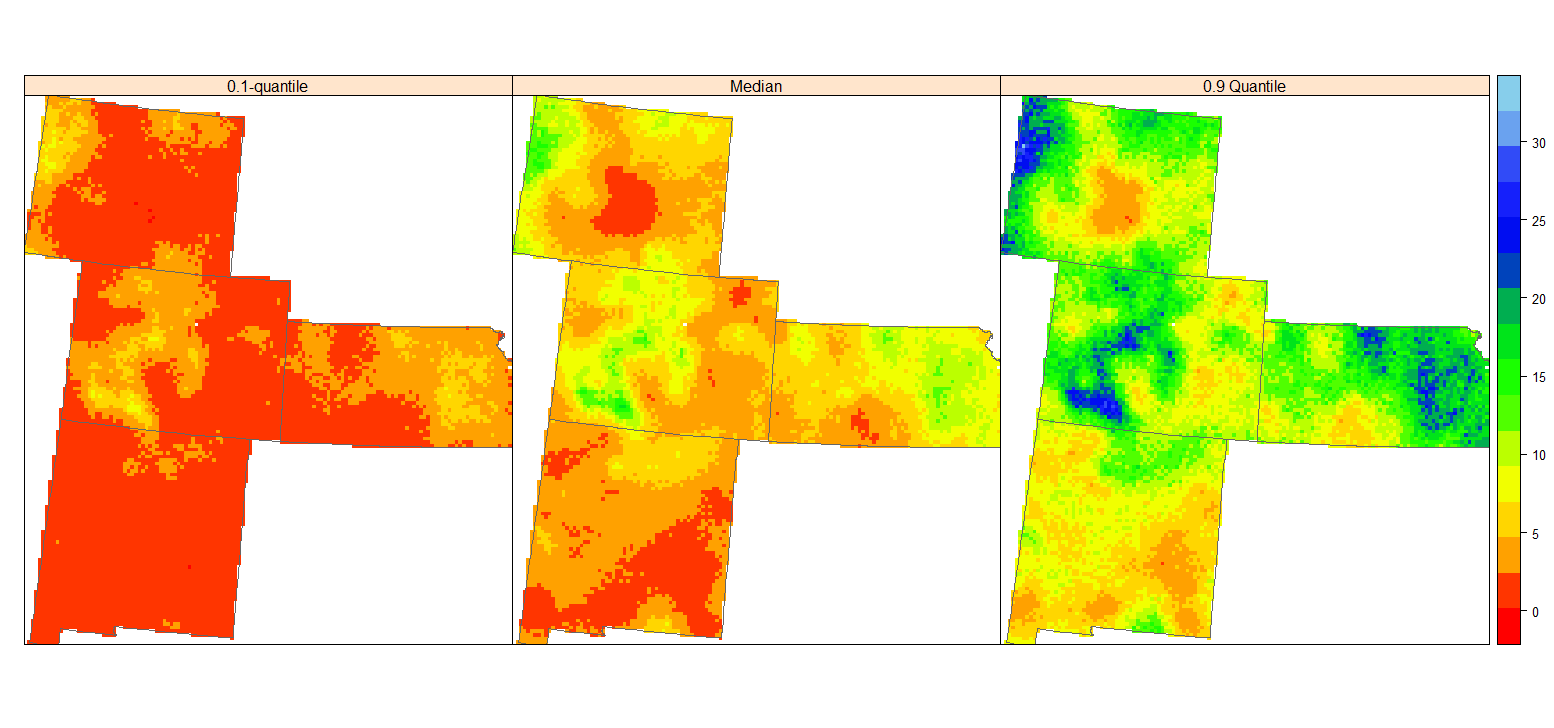
条件分位数图

  
spplot(grid.xy, c("q10","Median","q90"), sp.layout=list(bound), col.regions=col(20),
       names.attr = c("0.1-quantile", "Median","0.9 Quantile"), layout=c(3,1))

0.1 分位数图的高土壤碳 (黄色部分) 表示未知 SOC 浓度肯定较大的区域，而 0.9 图的低值部分 (深黄色) SOC 浓度肯定较小。

R, Spatial Interpolate

This post is licensed under CC BY 4.0 by the author.

交叉验证

数据变换

变异函数建模

K-fold 交叉验证

残差图

实际值 vs 预测值: 线性回归

1:1 绘图

留一交叉验证

使用独立数据集进行验证

数据变换-幂变换

变异函数建模

测试点的预测

计算残差

残差图

误差

实际值 vs 预测值: 线性回归

1:1 图

空间不确定性的条件模拟

数据变换-幂变换

变异函数建模

绘制变量图和拟合模型

普通克里金

条件高斯模拟

所有实现的半真实图

逆变换

空间不确定性的可视化

数据准备

动画地图

局部不确定性的度量

条件分位数图

Trending Tags